��Ŀ����
��֪��Բ
+
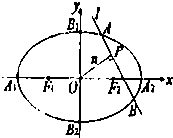
=1��a��b��0��������������ֱ�ΪF1��F2��p����Բ��һ�㣬����x���Ϸ���PF2��F1F2��PF2=��PF1���ˡ�[
��
]��
��1������Բ��������e��ȡֵ��Χ��
��2����eȡ���ֵʱ����F1��F2��P��ԲQ�Ľ�y����߶γ�Ϊ6������Բ�ķ��̣�
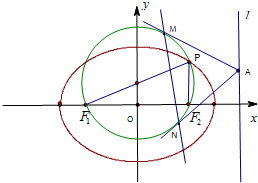
��3���ڣ�2���������£�����Բ����l����һ��A��ԲQ���������ߣ��е�ֱ�ΪM��N����̽��ֱ��MN�Ƿ�����㣿�������㣬������ö��㣻������˵�����ɣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| 1 |
| 2 |
��1������Բ��������e��ȡֵ��Χ��
��2����eȡ���ֵʱ����F1��F2��P��ԲQ�Ľ�y����߶γ�Ϊ6������Բ�ķ��̣�
��3���ڣ�2���������£�����Բ����l����һ��A��ԲQ���������ߣ��е�ֱ�ΪM��N����̽��ֱ��MN�Ƿ�����㣿�������㣬������ö��㣻������˵�����ɣ�

��1����=
=
����Ϊ2a2��-b2��=b2������Ϊ
=
��
��e2=
=1-
=1-
=
��
��e=
���ڦˡ�[
��
]�ϵ����ݼ���
����=
ʱ��e2��С
����=
ʱ��e2��С
����
��e2��
��
��
��e��
��
��2����e=
ʱ��
=
����c=b=
a��
��2b2=a2��
��PF2��F1F2����PF1��Բ��ֱ����Բ����PF1���е㣬����y���Ͻصõ��ҳ�����ֱ����
��PF1=6��
��|PF1|=2a-
=2a-
=
a=6��
��a=4��c=b=2
��
����Բ������
+
=1��
��3���ɣ�2���õ�|PF2|=
=
=2������Բ��Q��0��1�����뾶Ϊ3��ԲQ�ķ�����x2+��y-1��2=9����Բ�����߷���Ϊx=4
��
��ֱ��AM��AN��ԲQ���������ߣ����е�M��N����AQΪֱ����Բ�ϣ�
��A������Ϊ(4
��t)�����Բ����Ϊx(x-4
)+(y-1)(y-t)=0��
��ֱ��MN����Բ�Ĺ����ң���Բ��������ã�4
x+(t-1)y-8-t=0�������ֱ��MN�ķ��̣�
��ֱ��Ϊ��(y-1)t+4
x-y-8=0��
��
�����
��ֱ��MN�ع�����(
��1)��
| |PF2| |
| |PF1| |
| ||
2a-
|
| b2 |
| a2 |
| 2�� |
| 1+�� |
��e2=
| c2 |
| a2 |
| b2 |
| a2 |
| 2�� |
| 1+�� |
| 1-�� |
| 1+�� |
��e=
|
| 1 |
| 3 |
| 1 |
| 2 |
����=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
��
| ||
| 3 |
| ||
| 2 |
��2����e=
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| ||
| 2 |
��2b2=a2��
��PF2��F1F2����PF1��Բ��ֱ����Բ����PF1���е㣬����y���Ͻصõ��ҳ�����ֱ����
��PF1=6��
��|PF1|=2a-
| b2 |
| a |
| a2 |
| a |
| 3 |
| 2 |
��a=4��c=b=2
| 2 |
����Բ������
| x2 |
| 16 |
| y2 |
| 8 |
��3���ɣ�2���õ�|PF2|=
| b2 |
| a |
| a |
| 2 |
| 2 |
��ֱ��AM��AN��ԲQ���������ߣ����е�M��N����AQΪֱ����Բ�ϣ�
��A������Ϊ(4
| 2 |
| 2 |
��ֱ��MN����Բ�Ĺ����ң���Բ��������ã�4
| 2 |
��ֱ��Ϊ��(y-1)t+4
| 2 |
��
|
|
��ֱ��MN�ع�����(
9
| ||
| 8 |

��ϰ��ϵ�д�
 ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
�����Ŀ