题目内容
直线y=x与椭圆C:
+
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
+=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )A． | B． |
C． | D． |
A
设直线y=x与椭圆C: +=1在第一象限的交点为A,依题意得点A的坐标为(c,c),
又点A在椭圆C上,故有
+
=1,
因为b2=a2-c2,
所以+
=1,
所以c4-3a2c2+a4=0,
即e4-3e2+1=0,
所以e=
(e=
舍去).
故选A.
+=1在第一象限的交点为A,依题意得点A的坐标为(c,c),又点A在椭圆C上,故有
+=1,因为b2=a2-c2,
所以
+=1,所以c4-3a2c2+a4=0,
即e4-3e2+1=0,
所以e=
(e=舍去).故选A.
练习册系列答案
相关题目
直线
与抛物线
没有交点；
方程
表示椭圆；若
为真命题，试求实数
的取值范围.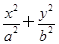
＝1(a>b>0)，F1、F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B.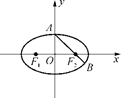
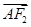＝2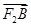
，
·
＝
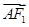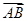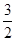，求椭圆的方程．
+
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
+
=1(a>b>0)的离心率为
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
+
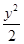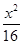=1
+
=1
+
=1
+
=1
的最小值是 .
+
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
(x+c)与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 .
表示的曲线为椭圆，则
的取值范围是（ ）
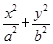＝1(a＞b＞0)的右焦点为F(3,0)，过点F的直线交E于A，B两点．若AB的中点坐标为(1，－1)，则E的方程为( )
＝1 
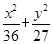＝1 
＝1 
＝1