题目内容
已知椭圆C: +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF= ,则C的离心率为( )
,则C的离心率为( )
 +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF= ,则C的离心率为( )
,则C的离心率为( )A.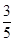 | B. | C. | D. |
B
|AF|2=|AB|2+|BF|2-2|AB|·|BF|cos∠ABF=100+64-2×10×8× =36,
=36,
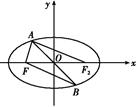
则|AF|=6,∠AFB=90°,
半焦距c=|FO|=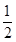 |AB|
|AB|
=5,
设椭圆右焦点F2,
连结AF2,
由对称性知|AF2|=|FB|=8,
2a=|AF2|+|AF|=6+8=14,
即a=7,
则e=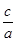 =
= .故选B.
.故选B.
 =36,
=36,
则|AF|=6,∠AFB=90°,
半焦距c=|FO|=
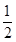 |AB|
|AB|=5,
设椭圆右焦点F2,
连结AF2,
由对称性知|AF2|=|FB|=8,
2a=|AF2|+|AF|=6+8=14,
即a=7,
则e=
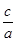 =
= .故选B.
.故选B.
练习册系列答案
相关题目
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点 ,离心率是
,离心率是 .
. 的标准方程;
的标准方程; 且与椭圆
且与椭圆 ,
, 两点,若
两点,若 ,求直线的方程.
,求直线的方程. +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
 的最小值是 .
的最小值是 . +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y= (x+c)与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 .
(x+c)与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 . 表示的曲线为椭圆,则
表示的曲线为椭圆,则 的取值范围是( )
的取值范围是( )



 =1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为
=1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为 的点P的个数为 .
的点P的个数为 . .
. =2
=2 ,求△AOB的面积.
,求△AOB的面积.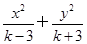 =1表示椭圆,则k的取值范围是________.
=1表示椭圆,则k的取值范围是________.