题目内容
在 中,
中, ,
, ,
, .
.
(1)求 长;
长;
(2)求 的值.
的值.
(1)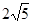 ,(2)
,(2)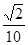 .
.
解析试题分析:(1)由已知 可得
可得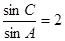 ,而由正弦定理:
,而由正弦定理: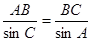 可得
可得
(2)由(1)及已知三角形的三边长都知道,所以由余弦定理可求cosA的值,从而sinA及sin2A和cos2A均可求得,由正弦的差角公式就很容易求得 的值.
的值.
试题解析:(1)解:在△ABC中,根据正弦定理,
于是AB=
(2)解:在△ABC中,根据余弦定理,得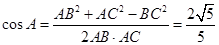
于是 sinA=
从而sin2A=2sinAcosA=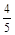 ,cos2A=cos2A-sin2A=
,cos2A=cos2A-sin2A=
所以 sin(2A-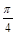 )=sin2Acos
)=sin2Acos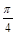 -cos2Asin
-cos2Asin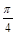 =
=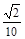
考点:1.正弦定理及余弦定理;2.三角恒等变形公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,若
,若
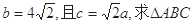 的面积.
的面积. ,求△ABC的面积.
,求△ABC的面积. 中,
中,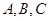 所对的边分别为
所对的边分别为 ,且
,且 ,
, .
. 的值;
的值; 的值.
的值.
 .
. ,n
,n ,试求|m
,试求|m n|的最小值.
n|的最小值. 上的奇函数,且在区间(0,
上的奇函数,且在区间(0, )上单调递增,若
)上单调递增,若 ,三
,三 角形的内角A满足
角形的内角A满足 ,则A的取值范围是
,则A的取值范围是  ,AC=2
,AC=2 ,cosC=
,cosC= .
.