题目内容
【题目】如图,在以![]() 为顶点的五面体中,面
为顶点的五面体中,面![]() 为正方形,
为正方形,![]() ,
,![]() ,且二面角
,且二面角![]() 与二面角
与二面角![]() 都是
都是![]() .
.
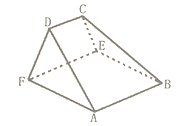
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;
(2)![]() .
.
【解析】
(1)推导出AF⊥DF,AF⊥FE,由线面垂直的判定定理即可证明AF⊥平面EFDC.
(2)过D作DG⊥EF,由DG⊥平面ABEF,以G为坐标原点,![]() 的方向为x轴正方向,|
的方向为x轴正方向,|![]() |为单位长度,建立空间直角坐标系G﹣xyz,利用向量法求出平面BCE的法向量,则可求得直线BF与平面BCE所成角的正弦值.
|为单位长度,建立空间直角坐标系G﹣xyz,利用向量法求出平面BCE的法向量,则可求得直线BF与平面BCE所成角的正弦值.
(1)![]() 面ABEF为正方形
面ABEF为正方形![]()
![]()
又![]()
![]()
![]() ,而
,而![]() ,
,
![]() 面
面![]() ,
,![]() 面
面![]()
![]()
![]() 面
面![]()
(2)![]()
![]()
![]() ,则由(1)知面
,则由(1)知面![]() 平面
平面![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]()
![]() 平面
平面![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长度,建立如图所示的空间直角坐标系
为单位长度,建立如图所示的空间直角坐标系![]() .
.
由(1)知![]() 为二面角
为二面角![]() 的平面角,故
的平面角,故![]() ,又
,又![]() ,则
,则![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() .
.
由已知,![]() ,
,![]()
![]() 平面
平面![]() .又平面
.又平面![]() 平面
平面![]() ,
,
故![]() ,
,![]() .由
.由![]() ,可得
,可得![]() 平面
平面![]() ,
,
![]()
![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() .
.![]()
![]() .
.
![]()
![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则 ,即
,即 ,
,
![]() 可取
可取![]() .
.
则 .
.
![]() 直线
直线![]() 与平面BCE所成角的正弦值为
与平面BCE所成角的正弦值为![]() .
.


【题目】学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
分组 | 频数 | 频率 |
[40,50) | A | 0.04 |
[50,60) | 4 | 0.08 |
[60,70) | 20 | 0.40 |
[70,80) | 15 | 0.30 |
[80,90) | 7 | B |
[90,100] | 2 | 0.04 |
合计 | C | 1 |

(1)在给出的样本频率分布表中,求A,B,C的值;
(2)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
(3)现从分数在[80,90),[90,100]的9名同学中随机抽取两名同学,求被抽取的两名学生分数均不低于90分的概率.
【题目】学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
分组 | 频数 | 频率 |
[40,50) | A | 0.04 |
[50,60) | 4 | 0.08 |
[60,70) | 20 | 0.40 |
[70,80) | 15 | 0.30 |
[80,90) | 7 | B |
[90,100] | 2 | 0.04 |
合计 | C | 1 |
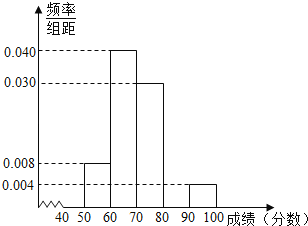
(1)在给出的样本频率分布表中,求A,B,C的值;
(2)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
(3)现从分数在[80,90),[90,100]的9名同学中随机抽取两名同学,求被抽取的两名学生分数均不低于90分的概率.