题目内容
12.若(ax+2b)6的展开式中x2与x3的系数之比为3:4,其中a>0,b≠0(1)当a=1时,求(ax+2b)6的展开式中二项式系数最大的项;
(2)令$F(a,b)=\frac{{{b^3}+16}}{a}$,求F(a,b)的最小值.
分析 (1)利用通项公式求得含x2的项和含x3的项,再根据展开式中x2与x3的系数之比为3:4,求得a=2b,再结合a=1求得展开式中二项式系数最大的项.
(2)利用导数求得F(b)的单调区间,再利用函数的单调性求得F(a,b)的最小值.
解答 解:(1)展开式中含x2的项为:240a2b4x2;展开式中含x3的项为:160a3b3x3,
结合题意可得:$\frac{{240{a^2}{b^4}}}{{160{a^3}{b^3}}}=\frac{3b}{2a}=\frac{3}{4},a=2b$
当a=1时,(ax+2b)6的展开式中二项式系数最大的项为${T_4}=C_6^3{x^3}=20{x^3}$.
(2)由a=2b,$F(b)=\frac{{{b^3}+16}}{2b}=\frac{b^2}{2}+\frac{8}{b}$,∴${F^'}(b)=b-\frac{8}{b^2}$.
当b∈(0,2)时,F′(b)<0; 当b∈(2,+∞)时,F′(b)>0,
所以 $F(b)=\frac{{{b^3}+16}}{2b}=\frac{b^2}{2}+\frac{8}{b}$在(0,2)递减,在(2,+∞)递增,
得F(a,b)的最小值为Fmin=F(2)=6,此时a=4,b=2.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,利用导数研究函数的单调性,由函数的单调性求函数的最值,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
3.若某人每次射击击中目标的概率均为$\frac{3}{5}$,此人连续射击三次,至少有两次击中目标的概率为( )
| A. | $\frac{81}{125}$ | B. | $\frac{54}{125}$ | C. | $\frac{36}{125}$ | D. | $\frac{27}{125}$ |
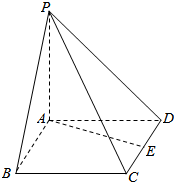 如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.