题目内容
11.已知命题p:“?x∈[-5,0],a≥ex”,命题q:“?x∈R,x2+4x+a=0”,若“p∧q”是真命题,则实数a的取值范围是( )| A. | [e,4] | B. | [1,4] | C. | (4,+∞) | D. | (-∞,1] |
分析 在命题p为真时,容易得出指数函数y=ex在[-5,0]上的最大值为1,从而有a≥1;在命题q为真时,便可知道一元二次方程x2+4x+a=0有解,根据△≥0,从而得出a≤4,而根据条件容易知道p,q都为真命题,从而求前面求出的两个a的范围的交集即可得出实数a的取值范围.
解答 解:命题p为真命题时,则:
∵y=ex为增函数;
∴该函数在[-5,0]上的最大值为1;
∴a≥1;
命题q为真时,则方程x2+4x+a=0有解;
∴△=16-4a≥0;
∴a≤4;
∵“p∧q”是真命题;
∴p,q都是真命题;
∴1≤a≤4;
∴实数a的取值范围为[1,4].
故选B.
点评 考查指数函数的单调性,根据函数的单调性求函数在闭区间上的最值,要分清?x和?x含义的区别,以及一元二次方程有解时△的取值情况,p∧q的真假和p,q真假的关系.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.已知复数z满足z•i=2-i,i为虚数单位,则z=( )
| A. | 2-i | B. | 1+2i | C. | -1+2i | D. | -1-2i |
3.若某人每次射击击中目标的概率均为$\frac{3}{5}$,此人连续射击三次,至少有两次击中目标的概率为( )
| A. | $\frac{81}{125}$ | B. | $\frac{54}{125}$ | C. | $\frac{36}{125}$ | D. | $\frac{27}{125}$ |
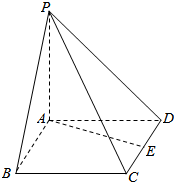 如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.