题目内容
18.设正项数列{an}的前n项和Sn满足2Sn=an2+an.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令${b_n}=\frac{n+1}{{{{(n+2)}^2}a_n^2}}$,数列{bn}的前n项和为Tn,证明:对于任意n∈N*,都有Tn<$\frac{5}{16}$.
分析 (I)利用递推式可得:$a_n^2-a_{n-1}^2-({a_n}+{a_{n-1}})=0$,因式分解即可得出;
(II)(Ⅱ)证明:由于an=n,可得${b_n}=\frac{n+1}{{{{(n+2)}^2}n_{\;}^2}}=\frac{1}{4}(\frac{1}{{n_{\;}^2}}-\frac{1}{{(n+2)_{\;}^2}})$,利用“裂项求和”、“放缩法”即可得出.
解答 (I)解:当n=1时,$2{a_1}=a_{{1^{\;}}}^2+{a_1}$,即a1=1,
当n≥2时,$2{S_n}=a_n^2+{a_n}$与$2{S_{n-1}}=a_{n-1}^2+{a_{n-1}}$相减
得:$2{a_n}=a_n^2+{a_n}-(a_{n-1}^2+{a_{n-1}})$,即$a_n^2-a_{n-1}^2-({a_n}+{a_{n-1}})=0$,
得:an+an-1=0或者an-an-1=1,
由an>0则an-an-1=1,
即数列{an}是以首项为1,公差为1的等差数列.
综上,数列{an}的通项an=n.
(Ⅱ)证明:由于an=n,
则${b_n}=\frac{n+1}{{{{(n+2)}^2}n_{\;}^2}}=\frac{1}{4}(\frac{1}{{n_{\;}^2}}-\frac{1}{{(n+2)_{\;}^2}})$,${T_n}=\frac{1}{4}[{1-\frac{1}{{3_{\;}^2}}+\frac{1}{{2_{\;}^2}}-\frac{1}{{4_{\;}^2}}+\frac{1}{{3_{\;}^2}}-\frac{1}{{5_{\;}^2}}+---+\frac{1}{{(n-1)_{\;}^2}}-\frac{1}{{(n+1)_{\;}^2}}+\frac{1}{{n_{\;}^2}}-\frac{1}{{(n+2)_{\;}^2}}}]$=$\frac{1}{4}[{1+\frac{1}{{2_{\;}^2}}-\frac{1}{{(n+1)_{\;}^2}}-\frac{1}{{(n+2)_{\;}^2}}}]$
<$\frac{1}{4}(1+\frac{1}{{2_{\;}^2}})=\frac{5}{16}$.
点评 本题考查了递推式的应用、等差数列的通项公式、“裂项求和”、“放缩法”、不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | $\frac{1}{2}$ |
| A. | 1+$\frac{1}{2}$i | B. | -1+$\frac{1}{2}$i | C. | -1-$\frac{1}{2}$i | D. | 1-$\frac{1}{2}$i |
| A. | $\sqrt{a}$-$\sqrt{b}$>$\sqrt{a-b}$ | B. | $\sqrt{a}$-$\sqrt{b}$<$\sqrt{a-b}$ | C. | $\sqrt{a}$-$\sqrt{b}$=$\sqrt{a-b}$ | D. | 无法确定 |
| A. | y=-2(x-30)(x-60) | B. | y=-2(x-30)(x-45) | C. | y=(x-45)2+450 | D. | y=-2(x-30)2+450 |
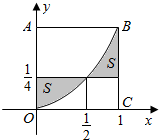 在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.
在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.