Question

【题目】某公司拟购买一块地皮建休闲公园，如图，从公园入口沿，方向修建两条小路，休息亭与入口的距离为米（其中为正常数），过修建一条笔直的鹅卵石健身步行带，步行带交两条小路于、处，已知，．

（1）设米，米，求关于的函数关系式及定义域；

（2）试确定，的位置，使三条路围成的三角形地皮购价最低．

Answer 1

【答案】(1) ，定义域为 (2)见解析

【解析】

（1）法一：由得，，进而得，得y关于x的函数关系即可；法二：由得，，，设，中，由正弦定理结合，求得y关于x的函数关系即可；(2) 设三条路围成地皮购价为元，地皮购价为元/平方米，则（为常数），利用换元法结合基本不等式求=最小值即可

（1）法一：由得，

且

由题可知

所以

得

即

所以

由得定义域为

法二： 由得，

设

中，由正弦定理

所以

同理可得

由

即

整理得，

由得定义域为

（2）设三条路围成地皮购价为元，地皮购价为元/平方米，则（为常数），

所以要使最小，只要使最小

由题可知

定义域为

令

则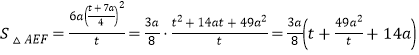

当且仅当即时取等号

所以，当时，最小，所以最小，此时y=

答：当点距离点 米,F距离点米远时，三条路围成地皮购价最低