题目内容
已知梯形ABCD中,AD∥BC,EF分别是BD,AC的中点.求证:EF∥BC,EF∥AD.
考点:平行线分线段成比例定理
专题:立体几何
分析:连结AE并延长交BC于点H,先证明△ADE≌△HBE,进而可得EF为△AHC的中位线,进而利用三角形中位线定理和平行公理证得答案.
解答:
证明:连结AE并延长交BC于点H
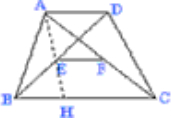
在△ADE和△HBE中,
∴△ADE≌△HBE
所以AE=EH,AD=BH
因为AF=CF
所以EF∥CH,
即EF∥BC,
又因为AD∥BC,
所以EF∥AD.

在△ADE和△HBE中,
|
∴△ADE≌△HBE
所以AE=EH,AD=BH
因为AF=CF
所以EF∥CH,
即EF∥BC,
又因为AD∥BC,
所以EF∥AD.
点评:本题考查的知识点是平行线分线段成比例定理,三角形中位线定理,本题的结论比较重要,要求理解并熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知m,n为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的是( )
| A、若l⊥m,l⊥n,且m,n?α,则l⊥α |
| B、若m∥n,n⊥α,则m⊥α |
| C、若m⊥α,m⊥n,则n∥α |
| D、若平面α内有不共线的三点到平面β的距离相等,则α∥β |