题目内容
在△ABC中,a=
,b=
,∠A=45°,求∠B,∠C及c.
| 2 |
| 3 |
考点:解三角形
专题:计算题,解三角形
分析:利用正弦定理求B,利用三角形的内角和求出c,再利用正弦定理,即可得出结论.
解答:
解:∵△ABC中,a=
,b=
,∠A=45°,
∴
=
,b>a,
∴sinB=
,
∴∠B=60°,
∴∠C=75°,
∴
=
,
∴c=2sin75°=
.
| 2 |
| 3 |
∴
| ||||
|
| ||
| sinB |
∴sinB=
| ||
| 2 |
∴∠B=60°,
∴∠C=75°,
∴
| c |
| sin75° |
| ||||
|
∴c=2sin75°=
| ||||
| 2 |
点评:本题考查正弦定理,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A,B两点,直线AF,BF分别与抛物线交于点C,D设直线AB,CD的斜率分别为k1,k2,则
等于( )
| k1 |
| k2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若把函数 y=sin(x+
)的图象向右平移m(m>0)个单位长度后,得到y=sinx的图象,则m的最小值( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
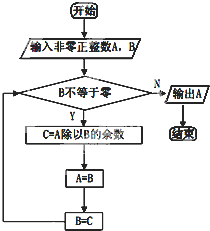 在如图的算法中,如果输入A=138,B=22,则输出的结果是( )
在如图的算法中,如果输入A=138,B=22,则输出的结果是( )| A、2 | B、4 | C、128 | D、0 |