题目内容
(文)已知向量
,
满足|
|=1,|
+
|=
,?
,
>=
,则|
|= .
| a |
| b |
| a |
| a |
| b |
| 7 |
| a |
| b |
| π |
| 3 |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意把|
+
|=
两边平方代入数据可得|
|的方程,解方程可得.
| a |
| b |
| 7 |
| b |
解答:
解:∵向量
,
满足|
|=1,|
+
|=
,<
,
>=
,
∴平方可得(
+
)2=7,即
2+2
•
+
2=7,
代入数据可得1+2×1×|
|×cos
+|
|2=7,
整理可得|
|2+|
|-6=0,即(|
|-2)(|
|+3)=0,
解得|
|=2或|
|=-3(舍去)
故答案为:2;
| a |
| b |
| a |
| a |
| b |
| 7 |
| a |
| b |
| π |
| 3 |
∴平方可得(
| a |
| b |
| a |
| a |
| b |
| b |
代入数据可得1+2×1×|
| b |
| π |
| 3 |
| b |
整理可得|
| b |
| b |
| b |
| b |
解得|
| b |
| b |
故答案为:2;
点评:本题考查平面向量数量积的运算,属基础题.

练习册系列答案
相关题目
已知函数f(x)=2sin(-2x+
)+1,若x∈(-
,
),则函数f(x)的值域为( )
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
A、(1-
| ||||
B、(1-
| ||||
C、[-1,1+
| ||||
| D、[-1,3] |
为了准备晚饭,小张找出了5种不同的新鲜蔬菜和4种冷冻蔬菜.如果晚饭时小张只吃1种蔬菜,不同的选择种数是( )
| A、5 | B、4 | C、9 | D、20 |
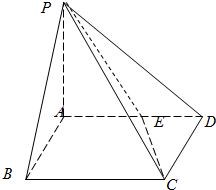 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.