题目内容
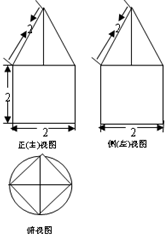
一空间几何体的三视图如图所示,则该几何体的体积为 .

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:上面是一个四棱锥,下面是一个圆柱.其中:四棱锥的母线长为2,底面是一个对角线为2的正方形;圆柱的底面直径为2,高为2.利用体积计算公式即可得出.
解答:
解:由三视图可知:上面是一个四棱锥,下面是一个圆柱.其中:四棱锥的母线长为2,底面是一个对角线为2的正方形;圆柱的底面直径为2,高为2.
∴该几何体的体积V=
×(
)2×
+π×12×2=2π+
.
故答案为:2π+
.
∴该几何体的体积V=
| 1 |
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
故答案为:2π+
2
| ||
| 3 |
点评:本题考查了四棱锥与圆柱的三视图及其体积计算公式,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
为了准备晚饭,小张找出了5种不同的新鲜蔬菜和4种冷冻蔬菜.如果晚饭时小张只吃1种蔬菜,不同的选择种数是( )
| A、5 | B、4 | C、9 | D、20 |
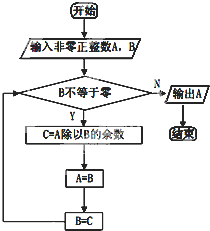 在如图的算法中,如果输入A=138,B=22,则输出的结果是( )
在如图的算法中,如果输入A=138,B=22,则输出的结果是( )| A、2 | B、4 | C、128 | D、0 |
若角α的终边上有一点P(m,2m),(m>0),则sinα的值是( )
A、
| ||||
B、-
| ||||
C、±
| ||||
| D、2 |