题目内容
(本小题满分12分)已知椭圆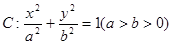 的离心率为
的离心率为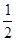 ,
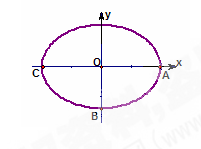
,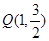 在椭圆C上,A,B为椭圆C的左、右顶点.
在椭圆C上,A,B为椭圆C的左、右顶点.
(1)求椭圆C的方程:
(2)若P是椭圆上异于A,B的动点,连结AP,PB并延长,分别与右准线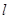 相交于M1,M2.问是否存在x轴上定点D,使得以M1M2为直径的圆恒过点D?若存在,求点D的坐标:若不存在,说明理由.
相交于M1,M2.问是否存在x轴上定点D,使得以M1M2为直径的圆恒过点D?若存在,求点D的坐标:若不存在,说明理由.
(1)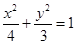 (2)存在
(2)存在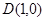 或
或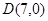 ,使得以
,使得以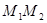 为直径的圆恒过点
为直径的圆恒过点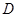
解析试题分析:(1)因为离心率为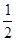 ,
,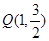 在椭圆上.所以利用待定系数法求出长半轴的长
在椭圆上.所以利用待定系数法求出长半轴的长 和短半轴的长
和短半轴的长 .从而写出椭圆的标准方程.本小题要求解方程组能力较强.虽然本小题属于较基础的题目,但是运算也是这道题难点,否则会影响到下一题的得分.
.从而写出椭圆的标准方程.本小题要求解方程组能力较强.虽然本小题属于较基础的题目,但是运算也是这道题难点,否则会影响到下一题的得分.
(2)通过假设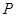 的坐标,写出直线
的坐标,写出直线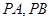 .并求出它们与准线方程的交点坐标.如果存在
.并求出它们与准线方程的交点坐标.如果存在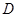 则点
则点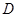 是在以线段
是在以线段 为直径的圆上,所以通过向量的垂直可得一个关于
为直径的圆上,所以通过向量的垂直可得一个关于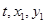 的等式.又因为
的等式.又因为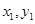 符合椭圆的方程.所以可以求出结论.
符合椭圆的方程.所以可以求出结论.
试题解析:(1)由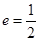 得:
得: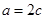 ,
,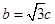 , 1分
, 1分
从而有: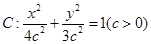
又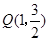 在椭圆
在椭圆 上,故有
上,故有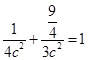 ,解得
,解得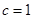
所以,椭圆 的方程为:
的方程为: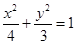 . 4分
. 4分
(2)设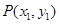 ,由(1)知:
,由(1)知: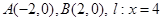 .
.
则直线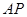 的方程为:
的方程为: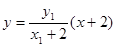 ,由
,由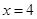 得
得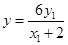 所以
所以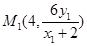 ;
;
同理得: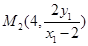 . 6分
. 6分
假设存在点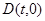 ,使得以
,使得以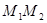 为直径的圆恒过点
为直径的圆恒过点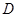
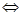
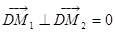
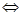
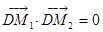 ,即:
,即: .
.
又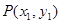 在椭圆
在椭圆 上,∴
上,∴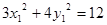 ∴
∴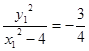 . 10分
. 10分
代入上式得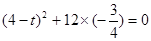 ,解得
,解得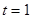 或7.
或7.
所以,存在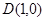 或
或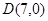 ,使得以
,使得以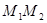 为直径的圆恒过点
为直径的圆恒过点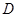 . 12分
. 12分
考点:1.待定系数求椭圆的方程.2.向量的数量积.3.知识的转化化归思想.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
 :
: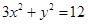 ,直线
,直线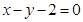 交椭圆
交椭圆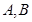 两点.
两点. 为直径的圆的方程.
为直径的圆的方程. 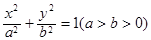 的左、右焦点分别为
的左、右焦点分别为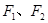 ,且
,且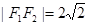 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.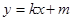 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点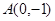 ,当
,当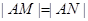 时,求实数m的取值范围,
时,求实数m的取值范围,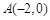 ,
, ,直线AG,BG相交于点G,且它们的斜率之积是
,直线AG,BG相交于点G,且它们的斜率之积是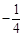 .
.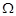 的方程;
的方程;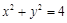 上有一个动点P,且P在x轴的上方,点
上有一个动点P,且P在x轴的上方,点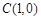 ,直线PA交(Ⅰ)中的轨迹
,直线PA交(Ⅰ)中的轨迹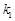 ,
,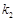 ,若
,若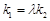 ,求实数
,求实数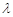 的取值范围.
的取值范围. 的两顶点坐标
的两顶点坐标 ,
,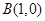 ,圆
,圆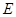 是
是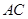 ,
,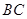 ,
, 上的切点分别为
上的切点分别为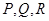 ,
,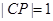 (从圆外一点到圆的两条切线段长相等),动点
(从圆外一点到圆的两条切线段长相等),动点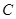 的轨迹为曲线
的轨迹为曲线 .
.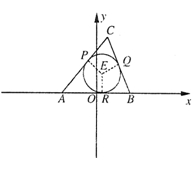
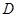 ,当点
,当点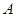 在以线段
在以线段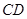 为直径的圆上时,求直线
为直径的圆上时,求直线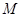 :
: 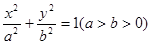 的离心率为
的离心率为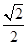 ,点
,点 (
( ,0),
,0), (0,
(0,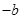 )原点
)原点 到直线
到直线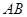 的距离为
的距离为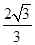 。
。
 为(
为(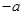 ,0),点
,0),点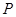 在椭圆
在椭圆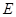 在直线
在直线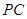 上,若直线
上,若直线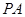 的方程为
的方程为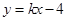 ,且
,且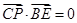 ,试求直线
,试求直线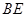 的方程.
的方程.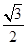 ,且经过点
,且经过点 ,直线
,直线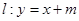 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B. 不过点M,求证:直线MA、MB与x轴围成一个等腰三角形
不过点M,求证:直线MA、MB与x轴围成一个等腰三角形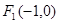 及
及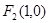 ,点
,点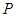 在以
在以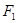 、
、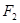 为焦点的椭圆
为焦点的椭圆 上,且
上,且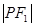 、
、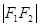 、
、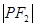 构成等差数列.
构成等差数列.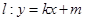 与椭圆
与椭圆 是直线
是直线 上的两点,且
上的两点,且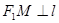 ,
,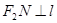 . 求四边形
. 求四边形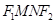 面积
面积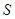 的最大值.
的最大值.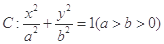 的离心率为
的离心率为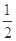 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线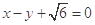 相切,过点P(4,0)且不垂直于x轴直线
相切,过点P(4,0)且不垂直于x轴直线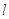 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点. 的取值范围;
的取值范围;