题目内容
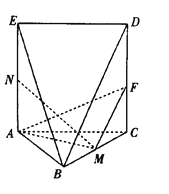
【题目】如图,边长为4的正方形![]() 中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,
中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,![]() 则
则![]() 的取值范围是_____________.
的取值范围是_____________.

【答案】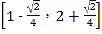
【解析】
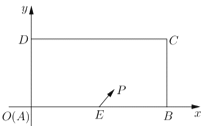
建立如图所示平面直角坐标系,可得![]() ,
,![]() =( 4,0),
=( 4,0),![]() .由图可知,当动圆Q的圆心经过点D时,P
.由图可知,当动圆Q的圆心经过点D时,P![]() .此时m+n取得最大值:4m+4n=8+
.此时m+n取得最大值:4m+4n=8+![]() ,可得m+n=2+
,可得m+n=2+![]() .当动圆Q的圆心为点C或点A时,利用三角函数求m+n的最小值.
.当动圆Q的圆心为点C或点A时,利用三角函数求m+n的最小值.
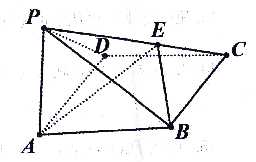
解:如图所示,边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及内部的动点,
向量![]() (m,n为实数),
(m,n为实数),
![]() =(0,4),
=(0,4),![]() =( 4,0),可得
=( 4,0),可得![]() =( 4m,4n).
=( 4m,4n).
当动圆Q的圆心经过点D时,如图:P![]() .
.
此时m+n取得最大值:4m+4n=8+![]() ,可得m+n=2+
,可得m+n=2+![]() .
.
当动圆Q的圆心为点C时,BP与⊙C相切且点P在x轴的下方时,![]() =(4+cosθ,sinθ),
=(4+cosθ,sinθ),
此时,4m+4n=4﹣![]() sin(θ+
sin(θ+![]() ),
),
m+n取得最小值为:1﹣![]() ,此时P( 4﹣
,此时P( 4﹣![]() ,﹣
,﹣![]() ).
).
同理可得,当动圆Q的圆心为点A时,BP与⊙A相切且点P在y轴的左方时,
m+n取得最小值为:1﹣![]() ,此时P(-
,此时P(-![]() ,4﹣
,4﹣![]() ).
).
∴则m+n的取值范围为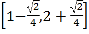
故答案为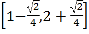 .
.

练习册系列答案
相关题目