题目内容
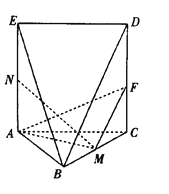
【题目】已知曲线M:![]() 的左、右顶点分别为A,B,设P是曲线M上的任意一点.
的左、右顶点分别为A,B,设P是曲线M上的任意一点.
(1)当P异于A,B时,记直线PA、PB的斜率分别为![]() 、
、![]() 则
则![]() 是否为定值,请说明理由.
是否为定值,请说明理由.
(2)已知点C在曲线M长轴上(异于A、B两点),且![]() 的最大值为7,求点C的坐标.
的最大值为7,求点C的坐标.
【答案】(1)k1k2![]() 为定值,证明见解析;(2)C(±3,0)
为定值,证明见解析;(2)C(±3,0)
【解析】
(1)由已知椭圆方程求出A,B的坐标,设P(x0,y0)(﹣4≤x0≤4),由斜率公式及点P在椭圆上即可证明k1k2是定值;
(2)设C(m,0)(﹣4<m<4),写出两点间的距离公式,利用配方法求最值,可得C的坐标.
(1)证明:由椭圆方程可得A(﹣4,0),B(4,0),
设P(x0,y0)(﹣4≤x0≤4),
则![]() ,
,![]() ,
,
∴k1k2 为定值;
为定值;
(2)设C(m,0)(﹣4<m<4),
则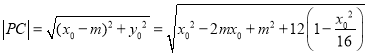
![]() .
.
若4m≥0,即m≥0,则![]() 7,解得m=3.
7,解得m=3.
此时C![]() ,
,
同理,若4m<0,可得m=﹣3,此时C![]() ,
,
故C点坐标为C(±3,0)

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目