题目内容
(本小题满分13分)
给定椭圆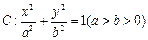 ,称圆心在坐标原点
,称圆心在坐标原点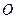 ,半径为
,半径为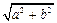 的圆是椭圆
的圆是椭圆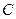 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为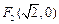 ,其短轴上的一个端点到
,其短轴上的一个端点到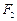 距离为
距离为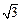 .
.
(Ⅰ)求椭圆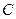 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)若过点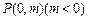 的直线
的直线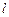 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且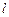 截椭圆C的“伴随圆”所得的弦长为
截椭圆C的“伴随圆”所得的弦长为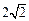 ,求
,求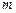 的值;
的值;
(Ⅲ)过椭圆C“伴椭圆”上一动点Q作直线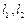 ,使得
,使得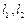 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线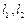 的斜率之积是否为定值,并说明理由.
的斜率之积是否为定值,并说明理由.
给定椭圆
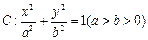 ,称圆心在坐标原点
,称圆心在坐标原点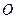 ,半径为
,半径为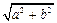 的圆是椭圆
的圆是椭圆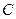 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为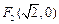 ,其短轴上的一个端点到
,其短轴上的一个端点到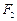 距离为
距离为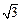 .
.(Ⅰ)求椭圆
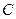 及其“伴随圆”的方程;
及其“伴随圆”的方程;(Ⅱ)若过点
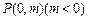 的直线
的直线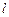 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且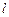 截椭圆C的“伴随圆”所得的弦长为
截椭圆C的“伴随圆”所得的弦长为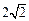 ,求
,求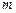 的值;
的值;(Ⅲ)过椭圆C“伴椭圆”上一动点Q作直线
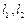 ,使得
,使得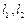 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线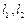 的斜率之积是否为定值,并说明理由.
的斜率之积是否为定值,并说明理由.解:(Ⅰ)由题意得: ,半焦距
,半焦距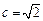
则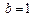 椭圆C方程为
椭圆C方程为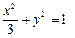
“伴随圆”方程为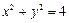
 ……………3分
……………3分
(Ⅱ)则设过点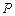 且与椭圆有一个交点的直线
且与椭圆有一个交点的直线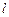 为:
为: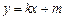 ,
,
则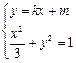 整理得
整理得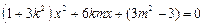
所以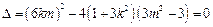 ,解
,解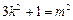 ① ……………5分
① ……………5分
又因为直线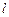 截椭圆
截椭圆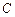 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为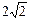 ,
,
则有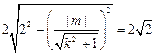 化简得
化简得 ② …………
② ………… …7分
…7分
联立①②解得, ,
,
所以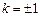 ,
,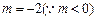 ,则
,则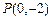 ……………8分
……………8分
(Ⅲ)当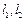 都有斜率时,设点
都有斜率时,设点 其中
其中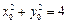 ,
,
设经过点 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为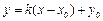 ,
,
由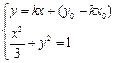 ,
, 消去
消去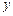 得到
得到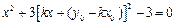 ……………9分
……………9分
即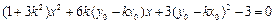 ,
, 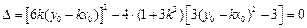 ,
, 
经过化简得到: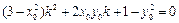 , ……………11分
, ……………11分
因为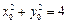 ,所以有
,所以有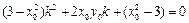 ,
,
设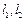 的斜率分别为
的斜率分别为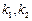 ,因为
,因为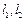 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,
所以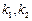 满足方程
满足方程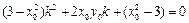 ,
,
因而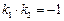 ,即直线
,即直线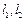 的斜率之积是为定值
的斜率之积是为定值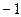 ……………13分
……………13分
 ,半焦距
,半焦距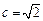
则
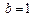 椭圆C方程为
椭圆C方程为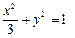
“伴随圆”方程为
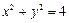
 ……………3分
……………3分(Ⅱ)则设过点
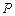 且与椭圆有一个交点的直线
且与椭圆有一个交点的直线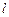 为:
为: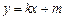 ,
, 则
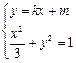 整理得
整理得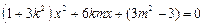
所以
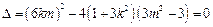 ,解
,解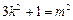 ① ……………5分
① ……………5分又因为直线
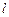 截椭圆
截椭圆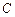 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为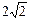 ,
,则有
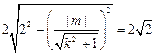 化简得
化简得 ② …………
② ………… …7分
…7分联立①②解得,
 ,
,所以
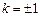 ,
,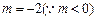 ,则
,则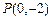 ……………8分
……………8分(Ⅲ)当
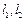 都有斜率时,设点
都有斜率时,设点 其中
其中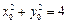 ,
,设经过点
 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为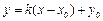 ,
,由
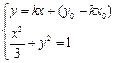 ,
, 消去
消去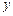 得到
得到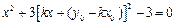 ……………9分
……………9分即
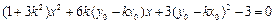 ,
, 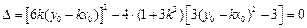 ,
, 
经过化简得到:
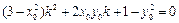 , ……………11分
, ……………11分因为
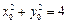 ,所以有
,所以有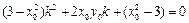 ,
,设
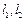 的斜率分别为
的斜率分别为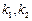 ,因为
,因为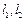 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,所以
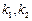 满足方程
满足方程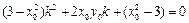 ,
,因而
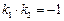 ,即直线
,即直线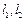 的斜率之积是为定值
的斜率之积是为定值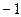 ……………13分
……………13分略

练习册系列答案
相关题目
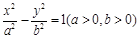 与直线
与直线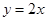 无交点,则离心率
无交点,则离心率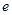 的取值范围是
的取值范围是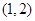
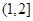
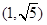
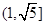
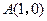 、
、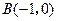 ,已知
,已知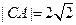 ,
,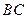 的垂直平分线
的垂直平分线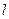 交
交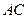 于
于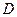 ,当点
,当点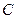 为动点时,点
为动点时,点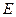 .
.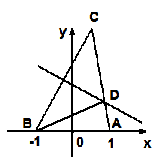
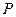 为
为 为坐标原点,曲线
为坐标原点,曲线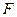 ,求
,求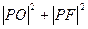 的最小值.
的最小值.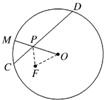
 )
)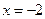 的距离比它到点F
的距离比它到点F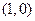 的距离大1,
的距离大1,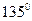 的直线交曲线C于A、B两点,求AB的长
的直线交曲线C于A、B两点,求AB的长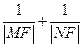 为定值
为定值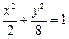 ,射线
,射线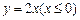 与椭圆的交点为
与椭圆的交点为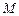 ,过
,过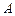 、
、 两点(异于
两点(异于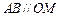 ;
; 面积的最大值.
面积的最大值.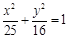 的离心率为
的离心率为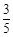
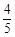
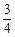
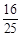
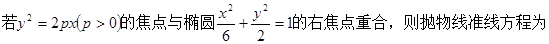 ( )
( )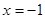
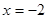
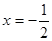
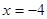
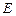 :
: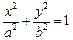 (
(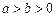 )过点
)过点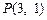 ,其左、右焦点分别为
,其左、右焦点分别为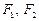 ,且
,且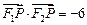 .
.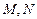 是直线
是直线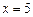 上的两个动点,且
上的两个动点,且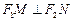 ,则以
,则以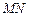 为直径的圆
为直径的圆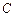 是否过定点?请说明理由.
是否过定点?请说明理由.