题目内容
已知椭圆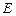 :
: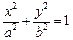 (
(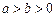 )过点
)过点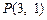 ,其左、右焦点分别为
,其左、右焦点分别为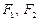 ,且
,且
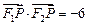 .
.
(1)求椭圆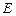 的方程;
的方程;
(2)若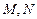 是直线
是直线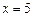 上的两个动点,且
上的两个动点,且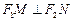 ,则以
,则以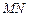 为直径的圆
为直径的圆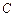 是否过定点?请说明理由.
是否过定点?请说明理由.
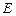 :
: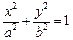 (
(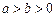 )过点
)过点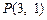 ,其左、右焦点分别为
,其左、右焦点分别为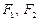 ,且
,且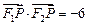 .
.(1)求椭圆
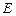 的方程;
的方程;(2)若
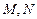 是直线
是直线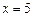 上的两个动点,且
上的两个动点,且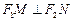 ,则以
,则以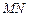 为直径的圆
为直径的圆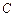 是否过定点?请说明理由.
是否过定点?请说明理由.解:(1)设点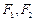 的坐标分别为
的坐标分别为 ,
,
则
故 ,可得
,可得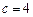 , …………………2分
, …………………2分
所以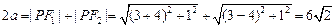 ,…………………4分
,…………………4分
故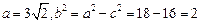 ,
,
所以椭圆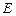 的方程为
的方程为 . ……………………………6分
. ……………………………6分
(2 )设
)设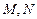 的坐标分别为
的坐标分别为 ,则
,则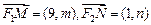 ,
,
又 ,可得
,可得 ,即
,即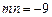 , …………………8分
, …………………8分
又圆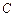 的圆心为
的圆心为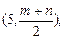 半径为
半径为 ,
,
故圆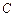 的方程为
的方程为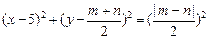 ,
,
 即
即 ,
,
也就是 , ……………………11分
, ……………………11分
令 ,可得
,可得 或2,
或2,
故圆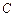 必过
必过 定点
定点 和
和 . ……………………13分
. ……………………13分
(另法:(1)中也可以直接将点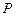 坐标代入椭圆方程来进行求解;(2)中可利用圆C直径的两端点直接写出圆
坐标代入椭圆方程来进行求解;(2)中可利用圆C直径的两端点直接写出圆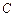 的方程)
的方程)
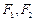 的坐标分别为
的坐标分别为 ,
,则

故
 ,可得
,可得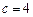 , …………………2分
, …………………2分所以
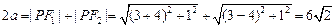 ,…………………4分
,…………………4分故
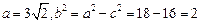 ,
,所以椭圆
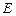 的方程为
的方程为 . ……………………………6分
. ……………………………6分(2
 )设
)设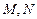 的坐标分别为
的坐标分别为 ,则
,则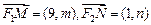 ,
,又
 ,可得
,可得 ,即
,即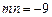 , …………………8分
, …………………8分又圆
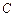 的圆心为
的圆心为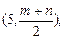 半径为
半径为 ,
,故圆
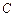 的方程为
的方程为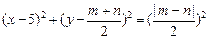 ,
,  即
即 ,
,也就是
 , ……………………11分
, ……………………11分令
 ,可得
,可得 或2,
或2,故圆
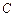 必过
必过 定点
定点 和
和 . ……………………13分
. ……………………13分(另法:(1)中也可以直接将点
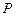 坐标代入椭圆方程来进行求解;(2)中可利用圆C直径的两端点直接写出圆
坐标代入椭圆方程来进行求解;(2)中可利用圆C直径的两端点直接写出圆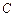 的方程)
的方程)略

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆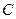 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为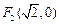 ,其短轴上的一个端点到
,其短轴上的一个端点到 距离为
距离为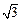 .
. 的直线
的直线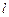 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且 ,求
,求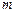 的值;
的值; ,使得
,使得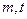 是实数,
是实数,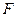 是抛物线
是抛物线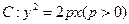 的焦点,直线
的焦点,直线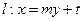 .
.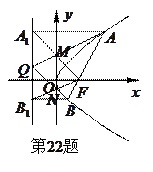 (1)若
(1)若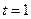 ,且
,且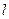 上,求抛物线
上,求抛物线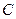 的方程;
的方程;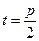 时,设直线
时,设直线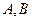 两点,过
两点,过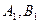 ,连
,连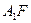 交
交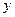 轴于点
轴于点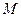 ,连结
,连结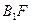 交
交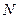 .
.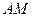 ⊥
⊥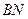 ;
;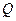 ,记△
,记△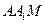 、四边形
、四边形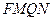 、△
、△ 的面积分别为
的面积分别为 ,问
,问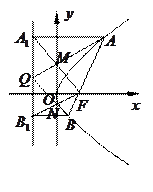 是否存在实数
是否存在实数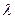 ,使
,使 成立?若存在,求出
成立?若存在,求出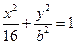
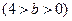 ,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.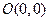 、
、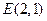 ,试探究是否存在这样的点
,试探究是否存在这样的点 :
: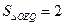 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由. ,直线
,直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 的垂线,垂足为点
的垂线,垂足为点 ,且
,且 .
. 的方程;
的方程;  使得过
使得过 的切线
的切线 与直线
与直线 平行?若存在,求出
平行?若存在,求出 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由. 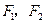 分别是椭圆
分别是椭圆
 的左、右焦点.若点
的左、右焦点.若点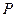 在椭圆上,且
在椭圆上,且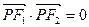 ,则
,则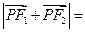
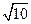
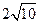

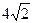
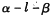 的平面角为
的平面角为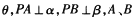 为垂足,PA =5,PB=4,点A、B到棱l的距离分别为x,y当θ变化时,点(x,y)的轨迹是下列
为垂足,PA =5,PB=4,点A、B到棱l的距离分别为x,y当θ变化时,点(x,y)的轨迹是下列 图形中的
图形中的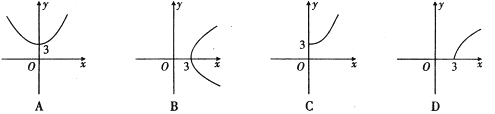
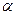 取何值,方程
取何值,方程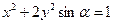 所表示的曲线一定不是( )
所表示的曲线一定不是( ) ,则点M的轨迹方程为 。
,则点M的轨迹方程为 。