题目内容
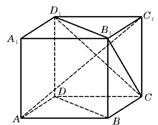
已知正方体ABCD-A1B1C1D1的棱长为1,动点P在正方体ABCD-A1B1C1D1表面上运动,且PA=r(0<r<
),记点P的轨迹的长度为f(r),则f(
)=______.(填上所有可能的值).
| 3 |
| 1 |
| 2 |
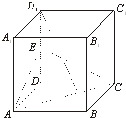
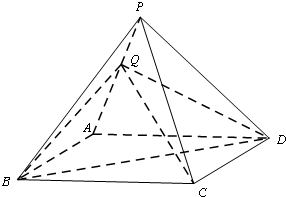
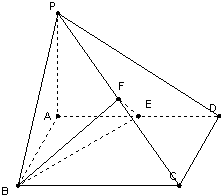
如图所示:①当0<r≤1时,f(r)=3×
×r=
r;∴f(
)=
.此时,由一次函数的单调性可得:0<f(r)≤
<5.
②当1<r≤
时,在平面ABCD内,设以点A为圆心,r为半径的圆弧与BC、CD分别交于点E、F,则cos∠DAF=
,∠EAF=
-2∠DAF,
∴cos∠EAF=sin2∠DAF=2×
×
=
,cos∠EAG=
=
,
∴f(r)=3rarccos
+3rayccos
;
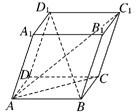
③当
<r<
时,∵CM=
,∴C1M=C1N=1-
,∴cos∠MAN=
=
,
∴f(r)=3rarccos
.
综上可知:当0<r≤1时,f(r)=
r;当1<r≤
时,f(r)=3rarccos
+3rayccos
;当
<r<
时,∴f(r)=3rarccos
.
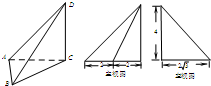
根据以上解析式及图性和对称性可得f(r)的图象:
由图象不难看出:函数y=f(r)与y=k的交点个数分别为,0,2,3,4.
故答案为f(
)=
.关于r的方程f(r)=k的解的个数可能为0,2,3,4.
| π |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
| 3π |
| 4 |
| 3π |
| 2 |

②当1<r≤
| 2 |
| 1 |
| r |
| π |
| 2 |
∴cos∠EAF=sin2∠DAF=2×
1-(
|
| 1 |
| r |
2
| ||
| r2 |
2r2-(
| ||||
| 2r2 |
| 1 |
| r2 |
∴f(r)=3rarccos
2
| ||
| r2 |
| 1 |
| r2 |
③当
| 2 |
| 3 |
| r2-2 |
| r2-2 |
2r2-[
| ||||
| 2r2 |
1+2
| ||
| r2 |
∴f(r)=3rarccos
1+2
| ||
| r2 |
综上可知:当0<r≤1时,f(r)=
| 3π |
| 2 |
| 2 |
2
| ||
| r2 |
| 1 |
| r2 |
| 2 |
| 3 |
1+2
| ||
| r2 |
根据以上解析式及图性和对称性可得f(r)的图象:

由图象不难看出:函数y=f(r)与y=k的交点个数分别为,0,2,3,4.
故答案为f(
| 1 |
| 2 |
| 3π |
| 4 |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目