题目内容
正四面体的四个顶点都在表面积为36π的一个球面上,则这个正四面体的高等于______.
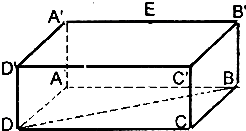
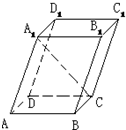
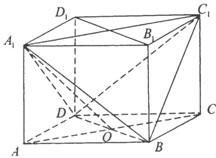
正四面体内接于球,则相应的一个正方体内接于球
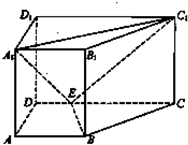
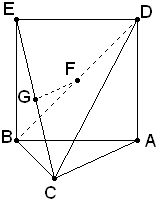
设正方体为ABCD-A1B1C1D1,则正四面体为ACB1D1
设球半径为R,则4πR2=36π,∴R=3
∴AC1=6,∴AD1=2
设底面ACB1中心为O,则AO=2
∴正四面体的高D1O=
=
=4
故答案为:4
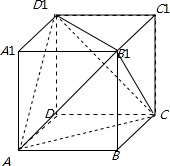
设正方体为ABCD-A1B1C1D1,则正四面体为ACB1D1
设球半径为R,则4πR2=36π,∴R=3
∴AC1=6,∴AD1=2
| 6 |
设底面ACB1中心为O,则AO=2
| 2 |
∴正四面体的高D1O=
| AD12-AO2 |
| 24-8 |
故答案为:4


练习册系列答案
相关题目