题目内容
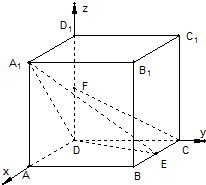
如图,正方体ABCD-A1B1C1D1的棱长为a,E为DD1的中点.
(1)求证:BD1∥平面EAC;
(2)求点D1到平面EAC的距离.
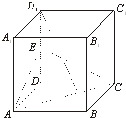
(1)求证:BD1∥平面EAC;
(2)求点D1到平面EAC的距离.

(1)证明:连接BD交AC于F,连EF.(1分)
因为F为正方形ABCD对角线的交点,
所长F为AC、BD的中点.(3分)
在DDD1B中,E、F分别为DD1、DB的中点,
所以EF∥D1B.(5分)
又EF?平面EAC,所以BD1∥平面EAC.(7分)
(2)设D1到平面EAC的距离为d.
在DEAC中,EF^AC,且AC=
a,EF=
a,
所以S△EAC=
EF•AC=
a2,
于是VD1-EAC=
dS△EAC=
a2d.(9分)
因为VA-ED1C=
AD•S△ED1C=
a×
×
a×a=
a3,(11分)
又VD1-EAC=VA-ED1C,即
a2d=
a3,(13分)
解得d=
a,故D1到平面EAC的距离为
a.(14分)
因为F为正方形ABCD对角线的交点,
所长F为AC、BD的中点.(3分)
在DDD1B中,E、F分别为DD1、DB的中点,
所以EF∥D1B.(5分)
又EF?平面EAC,所以BD1∥平面EAC.(7分)
(2)设D1到平面EAC的距离为d.
在DEAC中,EF^AC,且AC=
| 2 |
| ||
| 2 |
所以S△EAC=
| 1 |
| 2 |
| ||
| 4 |
于是VD1-EAC=
| 1 |
| 3 |
| ||
| 12 |
因为VA-ED1C=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
又VD1-EAC=VA-ED1C,即
| ||
| 12 |
| 1 |
| 12 |
解得d=
| ||
| 6 |
| ||
| 6 |

练习册系列答案
相关题目
 α, 则n
α, 则n