题目内容

若函数f（x）=kax-a-x，（a＞0，a≠1）在（-∞，+∞）上既是奇函数，又是增函数，则g（x）=loga（x+k）的是（　　）
A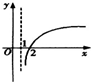．B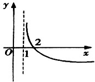．C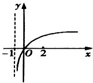．D．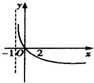
∵函数f（x）=kax-a-x，（a＞0，a≠1）在（-∞，+∞）上是奇函数
则f（-x）+f（x）=0
即（k-1）（ax-a-x）=0
则k=1
又∵函数f（x）=kax-a-x，（a＞0，a≠1）在（-∞，+∞）上是增函数
则a＞1
则g（x）=loga（x+k）=loga（x+1）
函数图象必过原点，且为增函数
故选C
练习册系列答案
相关题目
对任意a∈[-2，3]，不等式x2+（a-6）x+9-3a＞0恒成立，则实数x的取值范围是______．
已知不等式ax2+（a-1）x+a-1＜0对于所有的实数x都成立，求a的取值范围．
若奇函数f（x）是定义在（-1，1）上的减函数，且f（1-m）+f（1-2m）＜0，求实数m的取值范围．
定义在R上的偶函数f（x）满足f（x+1）=f（1-x）若当0≤x＜1时，f（x）=2x，则f（log26）=______．
下列函数在定义域上是奇函数，且在区间（-∞，0）上是增函数的是（　　）
A．y=x
1
3
B．y=x
1
2
C．y=x-2D．y=x
4
3
设f（x）是（-∞，+∞）上的奇函数，f（x+3）=f（x）．当0≤x≤1时有f（x）=2x，则f（8.5）=______．
设函数f(x)=log4(4x+1)+ax（a∈R）
（Ⅰ）若函数f（x）是定义在R上的偶函数，求a的值；
（Ⅱ）若不等式f（x）+f（-x）≥mt+m对任意x∈R，t∈[-2，1]恒成立，求实数m的取值范围．
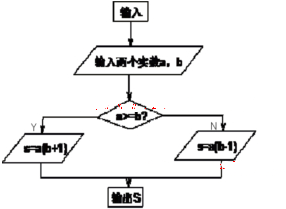
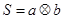定义某种运算,运算原理如图所示，则式子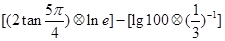的值为(     )
A．－3B．－4C．－8D．0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网