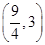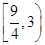题目内容
已知a、b、c分别是△ABC的三个内角A、B、C的对边.
(1)若△ABC面积S△ABC=
,c=2,A=60°,求a、b的值;
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
(1)若△ABC面积S△ABC=
| ||
| 2 |
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
(1)∵S△ABC=
bcsinA=
,
∴
b•2sin60°=
,得b=1,
由余弦定理得:a2=b2+c2-2bccosA=12+22-2×1×2•cos60°=3,
所以a=
.
(2)由余弦定理得:a=c•
,∴a2+b2=c2,
所以∠C=90°;
在Rt△ABC中,sinA=
,所以b=c•
=a,
所以△ABC是等腰直角三角形.
| 1 |
| 2 |
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
由余弦定理得:a2=b2+c2-2bccosA=12+22-2×1×2•cos60°=3,
所以a=
| 3 |
(2)由余弦定理得:a=c•
| a2+c2-b2 |
| 2ac |
所以∠C=90°;
在Rt△ABC中,sinA=
| a |
| c |
| a |
| c |
所以△ABC是等腰直角三角形.

练习册系列答案
相关题目
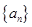 中,
中,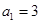 ,前
,前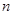 项和
项和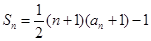 .
.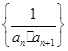 的前
的前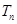 ,是否存在实数
,是否存在实数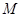 ,使得
,使得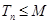 对一切正整数
对一切正整数

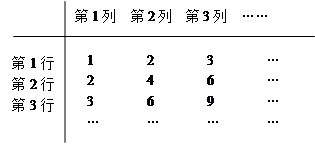
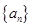 满足
满足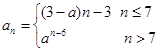 ,且
,且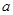 的取值范围是( )
的取值范围是( )