题目内容
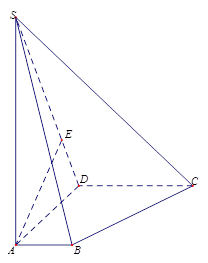
如图在四棱锥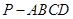 中,底面
中,底面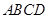 是矩形,
是矩形,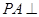 平面
平面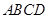 ,
,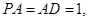
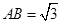 ,点
,点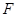 是
是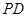 中点,点
中点,点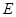 是
是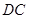 边上的任意一点.
边上的任意一点.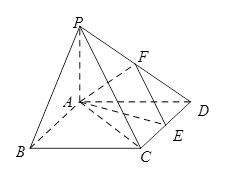
(1)当点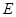 为
为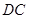 边的中点时,判断
边的中点时,判断 与平面
与平面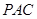 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)证明:无论点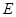 在
在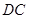 边的何处,都有
边的何处,都有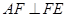 ;
;
(3)求三棱锥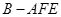 的体积.
的体积.
(1)答案详见解析;(2)答案详见解析;(3)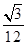 .
.
解析试题分析:(1)证明直线和平面平行的常用方法有两种:①证明直线和平面内的一条直线平行;②若两个平面平行,则一个平面内的直线平行于另一个平面.本题中,易证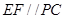 ,进而证明
,进而证明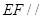 面
面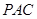 ;(2)要证明直线和直线垂直,往往通过证明直线和平面垂直.本题中,只需证明
;(2)要证明直线和直线垂直,往往通过证明直线和平面垂直.本题中,只需证明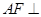 面
面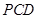 ,因
,因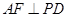 ,故只需证明
,故只需证明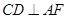 ,进而转化为证明
,进而转化为证明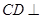 面
面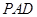 ,因
,因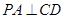 ,故只需证明
,故只需证明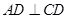 ,显然易证;(3)求四面体体积,难点是确定四面体的高,如果高不易求,可考虑等体积转化,本题中三棱锥
,显然易证;(3)求四面体体积,难点是确定四面体的高,如果高不易求,可考虑等体积转化,本题中三棱锥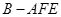 的体积可转化为
的体积可转化为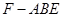 的体积来求.
的体积来求.
试题解析:(1)当点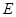 为
为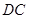 边的中点时,∵点
边的中点时,∵点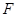 是
是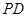 中点,∴
中点,∴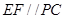 ,又∵
,又∵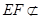 面
面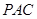 ,
,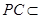 面
面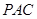 ,∴
,∴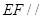 面
面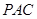 .
.
(2)∵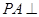 平面
平面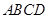 ,∴
,∴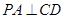 ,又∵底面
,又∵底面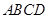 是矩形,∴
是矩形,∴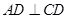 ,
,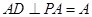 ,∴
,∴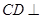 面
面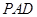 ,又∵
,又∵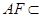 面
面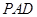 ,∴
,∴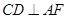 ,又
,又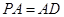 ,点
,点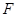 是
是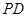 中点,∴
中点,∴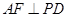 ,又
,又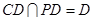 ,∴
,∴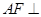 面
面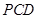 .
.
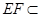 平面
平面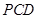 ,
,
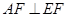 10分
10分
(3)作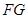 ∥
∥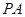 交
交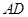 于
于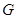 ,则
,则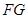
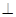 平面
平面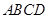 ,且
,且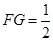

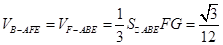
 三棱锥
三棱锥
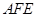 的体积为
的体积为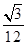 .14分
.14分
考点:1、直线和平面平行的判定;2、直线和平面垂直的判定和性质;3、四面体的体积.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 及其三视图如图所示,过棱
及其三视图如图所示,过棱 的中点
的中点 作平行于
作平行于 ,
,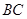 的平面分
的平面分 于点
于点 .
.
 是矩形;
是矩形; 的正弦值.
的正弦值. 中,
中, °,
°, ,
, 平面
平面 ,
, ,设
,设 的中点为
的中点为 ,
, .
.
 平面
平面 ;
; 的体积.
的体积.
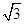 的正三棱锥
的正三棱锥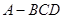 中,
中,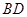 长为
长为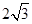 ,
,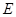 为棱
为棱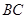 的中点,求
的中点,求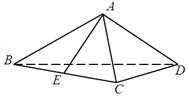
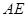 与
与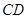 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.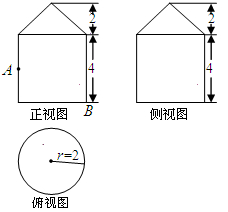
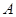 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点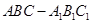 中,侧棱
中,侧棱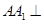 底面
底面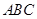 ,
, 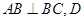 为
为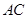 的中点,
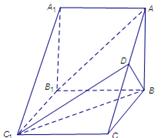
的中点,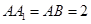 .
.
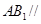 平面
平面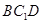 ;
;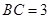 ,求三棱锥
,求三棱锥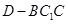 的体积.
的体积.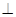 底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且
底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且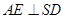
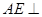 平面
平面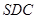 ;
;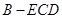 的体积
的体积