题目内容
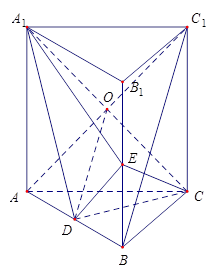
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
(1)证明:BC1//平面A1CD;
(2)设AA1=AC=CB=2,AB= ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
(1)详见解析;(2)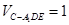 .
.
解析试题分析:(1)根据线面平行的判定定理,需在平面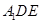 内找一条与
内找一条与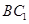 平行的直线.因为
平行的直线.因为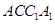 是矩形,故对角线互相平分,所以连结
是矩形,故对角线互相平分,所以连结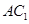 ,与
,与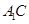 交于点O;因为D是AB的中点,连结
交于点O;因为D是AB的中点,连结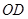 ,则
,则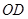 是
是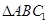 的中位线,所以
的中位线,所以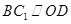 ,从而可证得
,从而可证得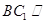 平面
平面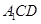 .(2)易得
.(2)易得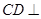 平面
平面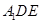 .所以
.所以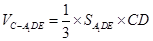 .因为
.因为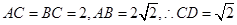 .求
.求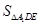 可用矩形的面积减去周围三个三角形的面积.从而求得三棱锥
可用矩形的面积减去周围三个三角形的面积.从而求得三棱锥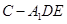 的体积..
的体积..
试题解析:(1)连结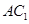 ,与
,与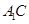 交于点O,连结
交于点O,连结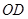 ,因为D是AB的中点,所以
,因为D是AB的中点,所以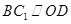 ,因为
,因为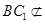 平面
平面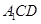 ,
,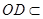 平面
平面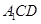 ,所以
,所以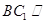 平面
平面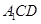 .
.
(2)因为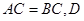 为
为 的中点,所以
的中点,所以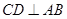 ,又因为该三棱柱是直三棱柱,所以
,又因为该三棱柱是直三棱柱,所以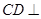 平面
平面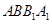 ,即
,即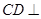 平面
平面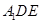 .所以
.所以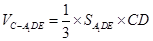 .因为
.因为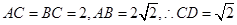 .
.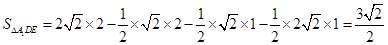 .所以
.所以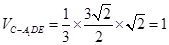 .
.
考点:1、空间直线与平面的平行关系;2、几何体的体积.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 及其三视图如图所示,平行于棱
及其三视图如图所示,平行于棱 的平面分别交四面体的棱
的平面分别交四面体的棱 于点
于点 .
.
 是矩形.
是矩形.
 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
 ,求证:
,求证: ;
; 的大小为
的大小为 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥 的体积为
的体积为 .
.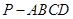 中,底面
中,底面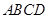 是矩形,
是矩形,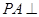 平面
平面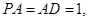
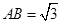 ,点
,点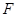 是
是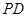 中点,点
中点,点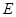 是
是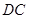 边上的任意一点.
边上的任意一点.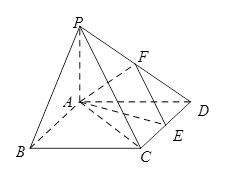
 与平面
与平面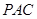 的位置关系,并加以证明;
的位置关系,并加以证明;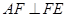 ;
;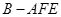 的体积.
的体积.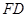 垂直于矩形
垂直于矩形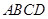 所在平面,
所在平面,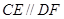 ,
, .
.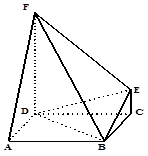
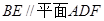 ;
; 的一个边
的一个边 ,
, ,则另一边
,则另一边 的长为何值时,三棱锥
的长为何值时,三棱锥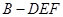 的体积为
的体积为 ?
?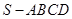 的底面是正方形,侧棱
的底面是正方形,侧棱 底面
底面 ,过
,过 作
作 垂直
垂直 交
交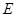 点,作
点,作 垂直
垂直 交
交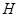 点,平面
点,平面 交
交 于
于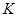 点,且
点,且 ,
, .
.
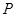 在何位置,都有
在何位置,都有 ;
;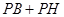 的最小值;
的最小值; 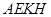 与平面
与平面 ,求证:
,求证: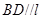 .
. 平面ABC.
平面ABC.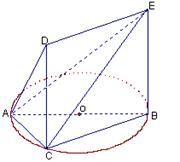
 ;
; ,
, ,
, ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.