题目内容
已知一个几何体的三视图如图所示.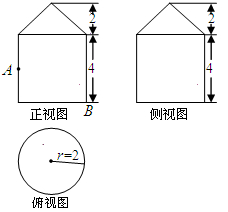
(1)求此几何体的表面积;
(2)在如图的正视图中,如果点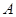 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点 到点
到点 的最短路径的长.
的最短路径的长.
(1)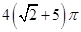 ;(2)
;(2)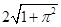 .
.
解析试题分析:(1)由三视图知:此几何体是一个圆锥和一个圆柱的组合体,底面圆半径长2,圆柱高为4,圆锥高为2,由此可求得该几何体的表面积;(2)将圆柱侧面展开,在平面矩形内线段 长为所求.
长为所求.
试题解析:(1)由三视图知:此几何体是一个圆锥加一个圆柱,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和,即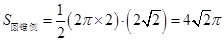 ,
,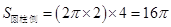 ,
,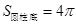 ,
,
所以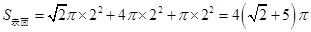 .
.
(2)沿 点与
点与 点所在母线剪开圆柱侧面,如图:
点所在母线剪开圆柱侧面,如图: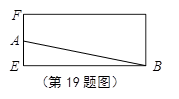
则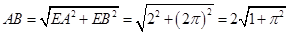 ,
,
所以从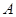 点到
点到 点在侧面上的最短路径的长为
点在侧面上的最短路径的长为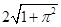 .
.
考点:1、多面体和旋转体表面上的最短距离问题;2、由三视图求面积、体积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.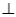 平面
平面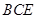 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
 中,已知
中,已知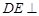 平面
平面 ,
,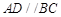 ,
,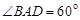 ,
, ,
, .
.
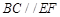 ;
;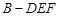 的体积.
的体积.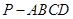 中,底面
中,底面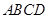 是矩形,
是矩形,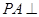 平面
平面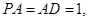
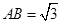 ,点
,点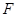 是
是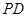 中点,点
中点,点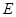 是
是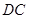 边上的任意一点.
边上的任意一点.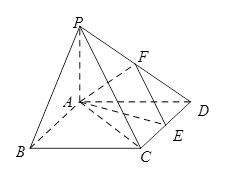
 与平面
与平面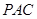 的位置关系,并加以证明;
的位置关系,并加以证明;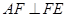 ;
;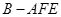 的体积.
的体积.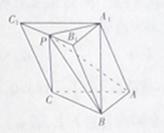
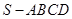 的底面是正方形,侧棱
的底面是正方形,侧棱 底面
底面 ,过
,过 作
作 垂直
垂直 交
交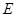 点,作
点,作 垂直
垂直 交
交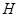 点,平面
点,平面 交
交 于
于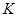 点,且
点,且 ,
, .
.
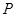 在何位置,都有
在何位置,都有 ;
;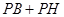 的最小值;
的最小值; 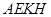 与平面
与平面 ,求证:
,求证: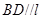 .
.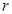 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?