题目内容
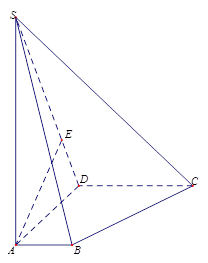
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA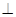 底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且
底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且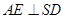
(1)证明: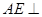 平面
平面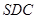 ;
;
(2)求三棱锥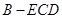 的体积
的体积
(1)详见解析;(2)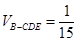
解析试题分析:(1)由于侧棱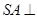 底面
底面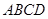 ,
,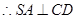 又
又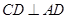 ,
,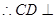 侧面
侧面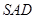 从而
从而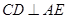 ,又因为
,又因为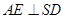 ,所以
,所以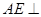 平面
平面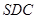 (2)
(2) 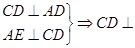 平面
平面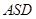 , 所以
, 所以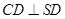 ,从而
,从而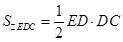 又由题设可得:
又由题设可得: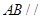 平面
平面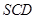 ,所以点B到平面SCD的距离等于点A到平面SCD的距离AE ,所以
,所以点B到平面SCD的距离等于点A到平面SCD的距离AE ,所以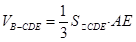
试题解析:(Ⅰ)证明: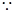 侧棱
侧棱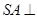 底面
底面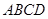 ,
,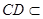 底面
底面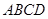
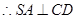 1分
1分
又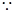 底面
底面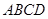 是直角梯形,
是直角梯形,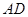 垂直于
垂直于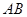 和
和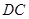
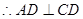 ,又
,又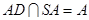
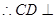 侧面
侧面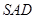 , 3分
, 3分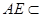 侧面
侧面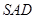
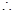
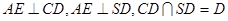
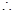
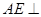 平面
平面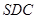 5分
5分
(2)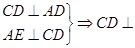 平面
平面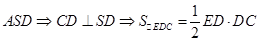 7分
7分
在 中
中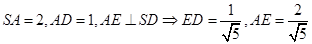
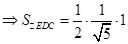 , 9分
, 9分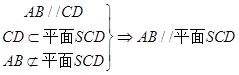 ,
,
所以点B到平面SCD的距离等于点A到平面SCD的距离AE 11分
所以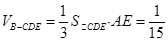 12分
12分
考点:1、空间直线与平面的位置关系;2、空间几何体的体积;3、二面角

练习册系列答案
相关题目
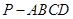 中,底面
中,底面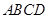 是矩形,
是矩形,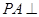 平面
平面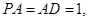
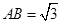 ,点
,点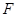 是
是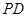 中点,点
中点,点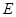 是
是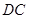 边上的任意一点.
边上的任意一点.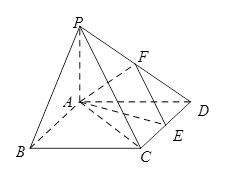
 与平面
与平面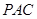 的位置关系,并加以证明;
的位置关系,并加以证明;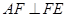 ;
;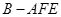 的体积.
的体积. 是边长为
是边长为 的正三角形,
的正三角形, ,
, 平面
平面 ,平面
,平面 平面
平面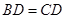 ,且
,且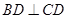 .
.
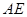 //平面
//平面 ;
; 平面
平面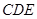 ;
;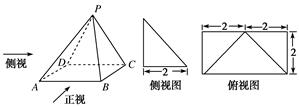

 中,AC⊥BC,AB⊥
中,AC⊥BC,AB⊥ ,
,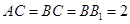 ,D为AB的中点,且CD⊥
,D为AB的中点,且CD⊥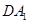 。
。
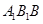 ⊥平面ABC;
⊥平面ABC;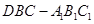 的体积。
的体积。

