题目内容
【题目】正方体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在![]() 上求一点
上求一点![]() ,使得
,使得![]() 平面
平面![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)以D为原点,DA,DC,D![]() 分别为x,y,z轴建立空间直角坐标系,
分别为x,y,z轴建立空间直角坐标系,
只需证明两平面的法向量数量积为0.(2)设![]() ,解得M(2,2λ,λ),由
,解得M(2,2λ,λ),由![]() 平面
平面![]() ,需
,需![]() ,可求解。
,可求解。
试题解析: 证明:(Ⅰ)建立如图所示的空间直角坐标系D-xyz,
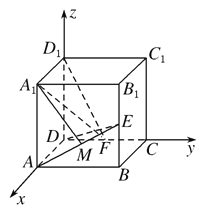
不妨设正方体的棱长为2,则A(2,0,0),E(2,2,1),F(0,1,0),A1(2,0,2), D1(0,0,2).
设平面AED的法向量为n1=(x1,y1,z1),则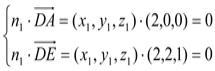
∴![]()
令y1=1,得n1=(0,1,-2).
同理可得平面A1FD1的法向量n2=(0,2,1).
∵n1·n2=0,
∴平面AED⊥平面A1FD1.
(Ⅱ)由于点M在AE上,
∴可设![]() =λ
=λ![]() =λ(0,2,1)=(0,2λ,λ),
=λ(0,2,1)=(0,2λ,λ),
可得M(2,2λ,λ),
于是![]() =(0,2λ,λ-2).
=(0,2λ,λ-2).
要使A1M⊥平面DAE,需A1M⊥AE,
∴![]() ·
·![]() =(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=
=(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=![]() .
.
故当AM=![]() AE时,即点M坐标为(2,
AE时,即点M坐标为(2,![]() ,
,![]() )时,A1M⊥平面DAE.
)时,A1M⊥平面DAE.

练习册系列答案
相关题目