题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xoy中,直线l的参数方程为 ![]() (t为参数,
(t为参数, ![]() ),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线
),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线 ![]()
(1)若直线l曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() 为定值;
为定值;
(2)将曲线 ![]() 上的任意点
上的任意点 ![]() 作伸缩变换
作伸缩变换 ![]() 后,得到曲线
后,得到曲线 ![]() 上的点
上的点 ![]() ,求曲线
,求曲线 ![]() 的内接矩形
的内接矩形 ![]() 周长的最大值.
周长的最大值.
【答案】
(1)解:曲线 ![]()
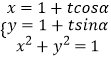
![]() ,
, ![]()
(2)解:伸缩变换后得 ![]() :
: ![]() .其参数方程为:
.其参数方程为: ![]() .
.
不妨设点 ![]() 在第一象限,由对称性知:周长为
在第一象限,由对称性知:周长为 ![]()
![]() ,(
,( ![]() 时取等号)周长最大为8
时取等号)周长最大为8
【解析】(1)由已知把直线的参数方程代入到圆的方程得到关于t的一元二次方程,借助韦达定理求出关系代入要求的式子即可得到结果。(2)根据伸缩变换转化可得出圆的标准方程,再转化为极坐标方程因为 A ( m , n ) 在第一象限由对称性可知周长为 4 ( m + n ) = 4 ( ![]() cos θ + sin θ ),整理成同名的三角函数式借助正弦函数的最值情况求出周长的最大值。
cos θ + sin θ ),整理成同名的三角函数式借助正弦函数的最值情况求出周长的最大值。

练习册系列答案
相关题目