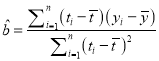题目内容
【题目】研究函数f(x)= ![]() 的性质,完成下面两个问题:
的性质,完成下面两个问题:
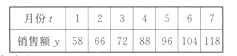
①将f(2),f(3),f(5)按从小到大排列为;
②函数g(x)= ![]() (x> 0)的最大值为 .
(x> 0)的最大值为 .
【答案】 f(5)<f(2)<f(3);![]()
【解析】①∵函数 ![]() ,∴
,∴ ![]() ,
,
f′(x)=0,可得:x=e,∴在(0,e)递增,(e,+∞)递减∴f(3)>f(5),
∵ ![]() ,∴f(2)>f(5)∵
,∴f(2)>f(5)∵ ![]() ∴f(3)>f(2)
∴f(3)>f(2)
故答案:f(5)<f(2)<f(3);
②∵函数 ![]() ,
,
∴ ![]()
令 ![]() ,
,
![]() ,x=e
,x=e
![]() ,x>e
,x>e
![]() ,0<x<e
,0<x<e
∴ ![]() 在(0,e)递增,在(e,+∞)递减,
在(0,e)递增,在(e,+∞)递减,
h(x)的极大值为 ![]() ,
,
∴函数 ![]() 的最大值为
的最大值为 ![]() .
.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】已知随机变量 ![]() 的取值为不大于
的取值为不大于 ![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中 ![]() (
( ![]() )满足:
)满足: ![]() ,且
,且 ![]() .
.
定义由 ![]() 生成的函数
生成的函数 ![]() ,令
,令 ![]() .
.
(I)若由 ![]() 生成的函数
生成的函数 ![]() ,求
,求 ![]() 的值;
的值;
(II)求证:随机变量 ![]() 的数学期望
的数学期望 ![]() ,
, ![]() 的方差
的方差 ![]() ;
;
( ![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量 ![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由 ![]() 生成的函数记为
生成的函数记为 ![]() ,求
,求 ![]() 的值.
的值.