题目内容
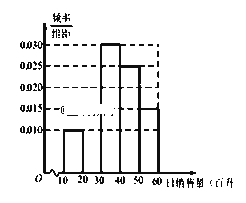
【题目】某加油站20名员工日销售量的频率分布直方图,如图所示:
(1)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在 [10,20),[20,30)的员工数;
(2)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在 [20,30)的概率.
【答案】(1)2,4(2)![]()
【解析】试题分析:(1)先根据频率分布直方图中所有小长方形面积和为1,得[20,30)的小矩形面积,根据小长方形面积等于组距与纵坐标的乘积得小矩形高度;根据小长方形面积等于对应区间概率得概率,再根据频数等于总数与频率乘积得结果;(2)先根据小长方形面积计算[10,20),[20,30)人数,根据枚举法确定总事件数,再确定两名员工日销量在 [20,30)的事件数,最后根据古典概型概率公式求概率.
试题解析:解:(Ⅰ)日销售量在[20,30)的频率为1﹣10×(0.010+0.030+0.025+0.015)=0.2,
故销售量在[20,30)的小矩形高度为=0.02,
∴频率分布图如上图所示:
日销售量在[10,20)的员工数为:20×10×0.010=2,
日销售量在[20,30)的员工数为:20×10×0.020=4.
(Ⅱ)由(Ⅰ)知日销售量在[10,30)的员工共有6人,在[10,20)的员工共有2人,令为a,b在[20,30)的员工有4人,令为c,d,e,f,从此6人中随机抽2人,基本事件为:![]()
![]() ,
,![]()
![]()
![]() 故基本事件 总数n=15,
故基本事件 总数n=15,
这2名员工日销售量在[20,30)包含的基本事件为:![]() ,
,![]() 个数m=6,
个数m=6,
∴这两名员工日销量在[20,30)的概率p=![]() .
.

练习册系列答案
相关题目
