题目内容
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示．已知两组技工在单位时间内加工的合格零件平均数都为9．
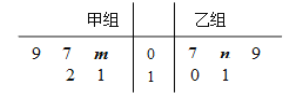
（1）分别求出
的值；
（2）分别求出甲、乙两组技工在单位时间内加工的合格零件的方差
和
，并由此分析两组技工的加工水平；
（3）质检部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，若两人加工的合格零件个数之和大于17，则称该车间“质量合格”，求该车间“质量合格”的概率．
【答案】（1）
（2）甲乙两组的整体水平相当，乙组更稳定一些（3）
【解析】
试题分析：（1）由两组技工在单位时间内加工的合格零件平均数都为9．利用茎叶图能求出m，n；（2）先分别求出
，
，由两组技工在单位时间内加工的合格零件平均数都为9，
，得到乙组技工加工水平高；（3）质监部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，设两人加工的合格零件数分别为（a，b），利用列举法能求出该车间“质量合格”的概率
试题解析：（1）∵两组技工在单位时间内加工的合格零件平均数都为9．
∴由茎叶图得：
(9+7+m+11+12)＝9
(7+n+9+10+11)＝9，
解得m=6，n=8．------------------------------2
（2）
，
，--------------4
∵
，
，∴甲乙两组的整体水平相当，乙组更稳定一些；-------6
（3）由题意，基本事件空间
,
，
，
，
，
，
，
，
，共计
个，而
的基本事件-----------8
A=
，
，
，
共计
个基本事件，故满足
的基本事件共有14，即该车间“质量合格”的基本事件有14个，----------------10
故该车间“质量合格”的概率为
．---------------12
