题目内容
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() (
(![]() )上,设
)上,设![]() ,
, ![]() ,
, ![]() 分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() (
(![]() )为椭圆
)为椭圆![]() 上两点,且满足
上两点,且满足![]() ,求证:
,求证: ![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可得结果;(Ⅱ)直线
,即可得结果;(Ⅱ)直线![]() 的方程为
的方程为![]() ,代入椭圆方程,并整理得
,代入椭圆方程,并整理得![]()
![]() ,根据韦达定理,弦长公式将、点到直线的距离公式将
,根据韦达定理,弦长公式将、点到直线的距离公式将![]() 的面积,用
的面积,用![]() 表示,再结合
表示,再结合![]()
![]() ,即可得结果.
,即可得结果.
试题解析:(Ⅰ)由题意,得直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() ,整理,得
,整理,得![]() .①
.①
又点![]() 在椭圆上,
在椭圆上, ![]() .②
.②
联立①②解得![]() ,
, ![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,并整理得
,代入椭圆方程,并整理得![]()
![]() .
.
![]()
![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]()
![]() .
.
又![]() ,则由题意,得
,则由题意,得![]()
![]()
![]() .
.
整理,得![]() ,则
,则![]()
![]() ,
,
整理,得![]() (满足
(满足![]() ).
).
![]()
![]()
![]()
![]()
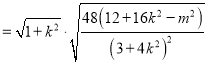
![]()
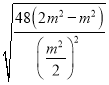
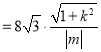 .
.
又点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
![]()
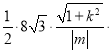
![]() ,为定值.
,为定值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目