题目内容
【题目】【2018河北保定市上学期期末调研】已知点![]() 到点
到点![]() 的距离比到
的距离比到![]() 轴的距离大1.
轴的距离大1.
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)设直线![]() :
: ![]() ,交轨迹
,交轨迹![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 为坐标原点,试在轨迹
为坐标原点,试在轨迹![]() 的
的![]() 部分上求一点
部分上求一点![]() ,使得
,使得![]() 的面积最大,并求其最大值.
的面积最大,并求其最大值.
【答案】(I)![]() 或
或![]() ;(II)
;(II)![]() .
.
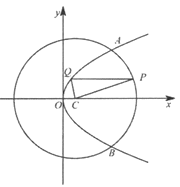
【解析】试题分析:(1)求轨迹方程可直接根据题意设点列等式化简即可或者根据我们所学的椭圆、双曲线、抛物线的定义取对比也行本题因为点M到点F(1,0) 的距离比到y轴的距离大1,所以点M到点F(1,0)的距离等于它到直线m:x=-1的距离由抛物线定义知道,点M的轨迹是以F为焦点,m为准线的抛物线或x轴负半轴;(2)根据题意先分析如何使![]() 的面积最大,可知当直线l的平行线与抛物线相切时△ABP的面积最大,然后根据点到线的距离公式求出高,弦长公式求出底,即得出面积
的面积最大,可知当直线l的平行线与抛物线相切时△ABP的面积最大,然后根据点到线的距离公式求出高,弦长公式求出底,即得出面积
解析:(1)因为点M到点F(1,0) 的距离比到y轴的距离大1,所以点M到点F(1,0)的距离等于它到直线m:x=-1的距离
由抛物线定义知道,点M的轨迹是以F为焦点,m为准线的抛物线或x轴负半轴
设轨迹C的方程为: ![]() ,
, ![]() ,
,
轨迹C方程为: ![]() , 或
, 或![]() .
.

(2)设A(x1,y1),B(x2,y2), P(x0,y0),
直线l化成斜截式为 ![]() ,当直线l的平行线与抛物线相切时△ABP的面积最大,
,当直线l的平行线与抛物线相切时△ABP的面积最大,
由图知P点在第四象限.抛物线在x轴下方的图象解析式: ![]() ,所以
,所以![]() ,
,
![]() ,解得
,解得![]() ,
, ![]() ,所以P点坐标
,所以P点坐标![]() ,P点到l的距离
,P点到l的距离![]() , A,B两点满足方程组
, A,B两点满足方程组 化简得
化简得![]() .
.
x1,x2 为该方程的根. 所以![]() ,
,
 ,
,
![]() .
.

练习册系列答案
相关题目