Question

【题目】已知f（x）=ax2+bx+c（a≠0）经过点（﹣1，0），（0，0），（1，2）．
（1）求f（x）的解析式；
（2）若数列{an}的前n项和Sn满足Sn=f（n），求{an}的通项公式．

Answer 1

【答案】
（1）解：将（﹣1，0），（0，0），（1，2）代入f（x）=ax2+bx+c得：

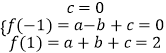，解得 ，

∴f（x）=x2+x；

（2）解：由（1）得：Sn=n2+n，

∴an=Sn﹣Sn﹣1=n2﹣n﹣[（n﹣1）2+（n﹣1）]=2n，

即{an}的通项公式是：an=2n

【解析】（1）根据待定系数法求出a，b，c的值，从而求出函数的解析式即可；（2）求出Sn ， 从而求出an即可．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．