Question

【题目】已知函数f(x)＝ax＋bx(a>0，b>0，a≠1，b≠1)．设a＝2，b＝.

（1）求方程f(x)＝2的根；

（2）若对于任意x∈R，不等式f(2x)≥mf(x)－6恒成立，求实数m的最大值；

Answer 1

【答案】（1）x＝0.（2）4

【解析】

（1）将a,b代入，计算求解即得解；

（2）通过将变量m分离出来，将问题转化为求分离出的函数的最小值则可.

（1）因为a＝2，b＝，所以f(x)＝2x＋2－x.

方程f(x)＝2，即2x＋2－x＝2，

亦即(2x)2－2×2x＋1＝0，所以(2x－1)2＝0，于是2x＝1，解得x＝0.

（2）由条件知：f(2x)＝22x＋2－2x＝(2x＋2－x)2－2＝(f(x))2－2.

因为f(2x)≥mf(x)－6对于x∈R恒成立，且f(x)>0，

所以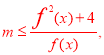对于一切实数R恒成立.而

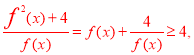
所以m≤4，故实数m的最大值为4.