题目内容
1.变量x,y满足约束条件:$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{kx+y-2k≤0}\end{array}\right.$,当k≥2时,对应的可行域面积为s,则z=$\frac{ks}{k+2}$的范围是[0,+∞).分析 作出不等式组对应的平面区域,求出可行域的面积s,结合分式的特点以及基本不等式进行求解即可.
解答 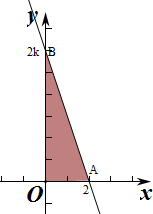 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
直线kx+y-2k=0过点A(2,0),B(0,2k),
则△的面积s=$\frac{1}{2}×2×2k$=2k,
则z=$\frac{ks}{k+2}$=$\frac{k•2k}{k+2}$=$\frac{2{k}^{2}}{k+2}$=$\frac{2(k+2)^{2}-8(k+2)+8}{k+2}$
=2(k+2)+$\frac{8}{k+2}$-8,
∵k≥2,∴k+2≥2,
设t=k+2,
则z=f(t)=2t+$\frac{8}{t}$-8=2(t+$\frac{4}{t}$)-8,在[2,+∞)上为增函数,
∴z=f(t)≥f(2)=2(2+2)-8=8-8=0,
即z≥0,
故z=$\frac{ks}{k+2}$的范围是[0,+∞),
故答案为:[0,+∞)
点评 本题主要考查不等式的应用,根据线性规划求出可行域的面积以及利用基本不等式是解决本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
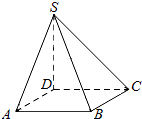 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2.