题目内容
【题目】设全集为R，集合A={x|-3＜x＜4}，B={x|1≤x≤10}．
（1）求A∪B，A∩（RB）；
（2）已知集合C={x|2a-1≤x≤a+1}，若C∩A=C，求实数a的取值范围．
【答案】（1）A∪B={x|-3＜x≤10}；A∩（RB）={x|-3＜x＜1} （2）（-1，+∞）
【解析】
（1）进行交集、并集和补集的运算即可；
（2）根据C∩A=C即可得出CA，从而可讨论C是否为空集：C=时，2a-1＞a+1；C≠时，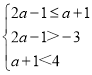
，解出a的范围即可．
（1）∵A={x|-3＜x＜4}，B={x|1≤x≤10}，
∴A∪B={x|-3＜x≤10}，RB={x|x＜1或x＞10}，A∩（RB）={x|-3＜x＜1}；
（2）∵C∩A=C，
∴CA，且C={x|2a-1≤x≤a+1}，
∴C=时，2a-1＞a+1，解得a＞2，
C≠时，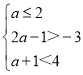
，解得-1＜a≤2，
综上得，实数a的取值范围为（-1，+∞）．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】某学校在九年级上学期开始时要掌握全年级学生每分钟跳绳的情况，随机抽取了100名学生进行测试，得到频率分布直方图（如图），且规定计分规则如下表：
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
（1）请估计学生的跳绳个数的众数和平均数（保留整数）；
（2）若从跳绳个数在
，
两组中按分层抽样的方法抽取9人参加正式测试，并从中任意选取2人，求2人得分之和不大于34分的概率.
