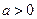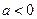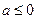题目内容
函数y=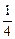 x4+
x4+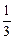 x3+
x3+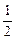 x2在[-1,1]上的最小值为
x2在[-1,1]上的最小值为
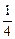 x4+
x4+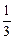 x3+
x3+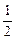 x2在[-1,1]上的最小值为
x2在[-1,1]上的最小值为| A.0 | B.-2 |
| C.-1 | D.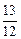 |
A
本题考查利用求导的方法求函数在闭区间上的最大值与最小值.比较极值点处的函数值与端点处函数值的大小,从而得解.
y′=x3+x2+x,令y′=0,解得x="0." 在[-1,1]上,列表如下:
所以ymin=f(0)="0," ymax=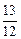 .
.
评注:在解求最值的选择题或填空题时,也可直接计算极值点与区间端点处的函数值,通过比较得解.
y′=x3+x2+x,令y′=0,解得x="0." 在[-1,1]上,列表如下:
| x | -1 | (-1,0) | 0 | (0,1) | 1 |
| y′ | -1 | - | 0 | + | 3 |
| y |  | 减函数 | 0 | 增函数 | 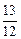 |
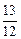 .
.评注:在解求最值的选择题或填空题时,也可直接计算极值点与区间端点处的函数值,通过比较得解.

练习册系列答案
相关题目
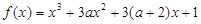 无极值,且对任意的
无极值,且对任意的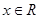 都有不等式
都有不等式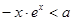 恒成立,则满足条件的实数
恒成立,则满足条件的实数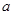 的取值范围是
的取值范围是



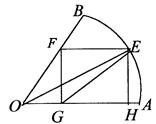
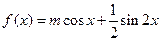 在
在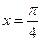 处取得极值,则
处取得极值,则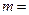 .
.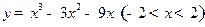 有( )
有( )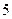 ,极小值
,极小值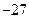 ,B 极大值
,B 极大值 ,C 极大值
,C 极大值 有极值的充要条件是( )
有极值的充要条件是( )