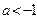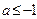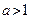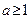题目内容
.f(x)=x(x-c)2在x=2处有极大值,则常数c的值为____________.
6
本题考查多项式函数的导数及函数极值的概念.
由f(x)=x(x2-2cx+c2)=x3-2cx2+c2x,
∴f′(x)=3x2-4cx+c2=(3x-c)(x-c).
令f′(x)=0,得x1=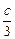 ,x2=c.
,x2=c.
(1)当c>0时,
由题意知,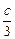 =2,得c=6.
=2,得c=6.
(2)当c<0时,在x=c处取极大值,不合题意.所以c=6.
由f(x)=x(x2-2cx+c2)=x3-2cx2+c2x,
∴f′(x)=3x2-4cx+c2=(3x-c)(x-c).
令f′(x)=0,得x1=
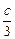 ,x2=c.
,x2=c.(1)当c>0时,
| x | (-∞,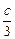 ) ) | 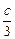 | (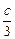 ,c) ,c) | c | (c,+∞) |
| y′ | + | 0 | - | 0 | + |
| y | ↗ | 极大值 | ↘ | 极小值 | ↗ |
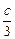 =2,得c=6.
=2,得c=6.(2)当c<0时,在x=c处取极大值,不合题意.所以c=6.

练习册系列答案
相关题目
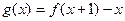 的最大值;
的最大值; 时,求证
时,求证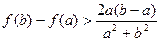 ;
;

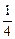 x4+
x4+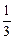 x3+
x3+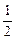 x2在[-1,1]上的最小值为
x2在[-1,1]上的最小值为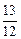
 在
在 时取得极值,且
时取得极值,且 。(1)试求常数
。(1)试求常数 值;(2)试判断
值;(2)试判断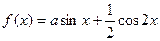 (
(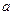 为常数)在
为常数)在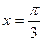 处取得极值,则
处取得极值,则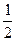
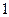
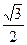
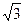
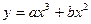 ,当
,当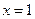 时,有极大值
时,有极大值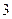 ;
;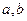 的值;(2)求函数
的值;(2)求函数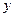 的极小值。
的极小值。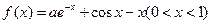 若对任意的
若对任意的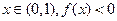 恒成立,则
恒成立,则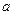 的取值范围( )
的取值范围( )