题目内容
5.在△ABC中,角A,B,C所对的边分别为a,b,c.且cosB=-$\frac{1}{2}$.(Ⅰ)若a=2,b=2$\sqrt{3}$,求角C;
(Ⅱ)求sinA•sinC的取值范围.
分析 (1)利用正弦定理可解出A,在利用内角和解出C;
(2)由A+C=$\frac{π}{3}$可将sinA•sinC化为sin($\frac{π}{3}$-C)•sinC,然后借助三角恒等变换化成关于C的三角函数
解答 解:(1)在△ABC中,∵cosB=-$\frac{1}{2}$,B∈(0,π),
∴B=$\frac{2π}{3}$,sinB=$\frac{\sqrt{3}}{2}$.
由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$,可得
$\frac{2}{sinA}=\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$,∴sinA=$\frac{1}{2}$.
又∵B=$\frac{2π}{3}$,∴A=$\frac{π}{6}$.
∴C=π-A-B=$\frac{π}{6}$.
(2)sinA•sinC=sin($\frac{π}{3}$-C)•sinC
=($\frac{\sqrt{3}}{2}$cosC-$\frac{1}{2}$sinC)•sinC
=$\frac{\sqrt{3}}{4}$sin2C+$\frac{1}{4}$cos2C-$\frac{1}{4}$
=$\frac{1}{2}$sin(2C+$\frac{π}{6}$)-$\frac{1}{4}$
∵C∈(0,$\frac{π}{3}$),
∴2C+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$).
∴sin(2C+$\frac{π}{6}$)∈($\frac{1}{2}$,1].
∴sinA•sinC的取值范围是(0,$\frac{1}{4}$].
点评 本题考查了解三角形和三角函数恒等变换,属于中档题.

练习册系列答案
相关题目
16.设a,b是实数,则“ab>0”是“a+b>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件已知 |
13.已知p:?x∈R,x2-x+1>0,q:?x∈(0,+∞),sinx>1,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∨q | C. | p∨¬q | D. | ¬p∧¬q |
14.若sinα=-$\frac{\sqrt{10}}{10}$,且α为第四象限角,则tanα的值等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
15.sin2(π+α)-cos(π+α)cosα+1的值是( )
| A. | 2 | B. | 1 | C. | 2sin2α | D. | 0 |
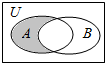 已知全集U=R,集合A={0,1,2},B={x∈Z|x2≤3},如图阴影部分所表示的集合为{2}.
已知全集U=R,集合A={0,1,2},B={x∈Z|x2≤3},如图阴影部分所表示的集合为{2}.