题目内容
12.$tan({\frac{3π}{4}+α})=3$,则tanα=-2,$\frac{sinα}{{{{cos}^3}α}}$=-10.分析 利用两角和的正切函数求出正切函数值,然后化简所求的表达式为正切函数的形式,即可求出结果.
解答 解:$tan({\frac{3π}{4}+α})=3$,
可得$\frac{tan\frac{3π}{4}+tanα}{1-tan\frac{3π}{4}tanα}$=3.
即:$\frac{-1+tanα}{1+tanα}$=3,
解得tanα=-2.
$\frac{sinα}{{{{cos}^3}α}}$=$\frac{{sin}^{3}α+sin{αcos}^{2}α}{{cos}^{3}α}$=tan3α+tanα=-8-2=-10.
故答案为:-2;-10;
点评 本题考查三角函数的化简求值,两角和的正切函数的应用,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.如图,给出了偶函数y=f(x)的局部图象,根据图象信息下列结论正确的是( ) 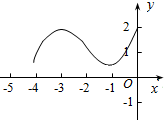

| A. | f(-1)-f(2)>0 | B. | f(1)-f(-2)=0 | C. | f(1)-f(2)<0 | D. | f(-1)+f(2)<0 |
4.已知函数f(x)=ax2+bx+c(a>0),对于任意的x1,x2(x1≠x2),则$f(\frac{{{x_1}+{x_2}}}{2})$与$\frac{{f({x_1})+f({x_2})}}{2}$的大小关系是( )
| A. | $f(\frac{{{x_1}+{x_2}}}{2})$<$\frac{{f({x_1})+f({x_2})}}{2}$ | B. | $f(\frac{{{x_1}+{x_2}}}{2})$>$\frac{{f({x_1})+f({x_2})}}{2}$ | ||
| C. | $f(\frac{{{x_1}+{x_2}}}{2})$=$\frac{{f({x_1})+f({x_2})}}{2}$ | D. | 无法确定 |