题目内容
9．已知函数$f（x）=\left\{{\begin{array}{l}{|{{log}_2}x|，}&{（0＜x＜4）}\\{-\frac{1}{2}x+6，}&{（x≥4）}\end{array}}\right.$，若方程f（x）-k=0有三个不同的解a，b，c，且a＜b＜c，则ab+c的取值范围是（11，13）．分析 先画出图象，再根据条件即可求出其范围．不妨设a＜b＜c，利用f（a）=f（b）=f（c），可得-log2a=log2b=-$\frac{1}{2}$c+6，由此可确定ab+c的取值范围．
解答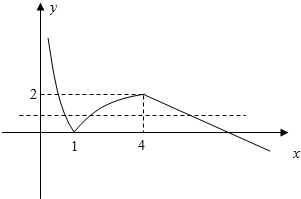 
解：根据已知画出函数图象：
∵f（a）=f（b）=f（c），∴-log2a=log2b=-$\frac{1}{2}$c+6，
∴log2（ab）=0，0＜-$\frac{1}{2}$c+6＜2，
解得ab=1，10＜c＜12，
∴11＜ab+c＜13．
故答案为：（11，13）．
点评 本题考查分段函数，考查绝对值函数，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
19．抽取某种型号的车床生产的10个零件，编号为A1，A2，…，A10，测量其直径（单位：cm），得到下面数据：
其中直径在区间[1.49，1.51]内的零件为一等品．
（1）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（2）从一等品零件中，随机抽取2个．
①用零件的编号列出所有可能的抽取结果；
②求这2个零件直径相等的概率；
（3）若甲、乙分别从一等品中各取一个，求甲取到零件的直径大于乙取到零件的直径的概率．
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.48 | 1.47 | 1.53 | 1.52 | 1.47 |
（1）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（2）从一等品零件中，随机抽取2个．
①用零件的编号列出所有可能的抽取结果；
②求这2个零件直径相等的概率；
（3）若甲、乙分别从一等品中各取一个，求甲取到零件的直径大于乙取到零件的直径的概率．
4．已知函数f（x）=ax2+bx+c（a＞0），对于任意的x1，x2（x1≠x2），则$f（\frac{{{x_1}+{x_2}}}{2}）$与$\frac{{f（{x_1}）+f（{x_2}）}}{2}$的大小关系是（ ）
| A． | $f（\frac{{{x_1}+{x_2}}}{2}）$＜$\frac{{f（{x_1}）+f（{x_2}）}}{2}$ | B． | $f（\frac{{{x_1}+{x_2}}}{2}）$＞$\frac{{f（{x_1}）+f（{x_2}）}}{2}$ | ||
| C． | $f（\frac{{{x_1}+{x_2}}}{2}）$=$\frac{{f（{x_1}）+f（{x_2}）}}{2}$ | D． | 无法确定 |
14．若sinα=-$\frac{\sqrt{10}}{10}$，且α为第四象限角，则tanα的值等于（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |