题目内容
在平面直角坐标系 中,动点
中,动点 到两点
到两点 、
、 的距离之和等于4.设点
的距离之和等于4.设点 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)设直线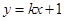 与
与 交于
交于 、
、 两点,若
两点,若 ,求
,求 的值.
的值.
(1)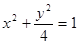 ;(2)
;(2) .
.
解析试题分析:(1)根据点 到两点
到两点 、
、 的距离之和等于4,由椭圆定义可知,点
的距离之和等于4,由椭圆定义可知,点 的轨迹
的轨迹 是以
是以 、
、 为焦点,长半轴为2的椭圆,由此可求曲线
为焦点,长半轴为2的椭圆,由此可求曲线 的方程;
的方程;
(2)设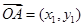 ,
, ,利用
,利用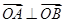 ,可得
,可得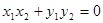 ,把
,把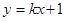 代入椭圆方程,消去
代入椭圆方程,消去 可得
可得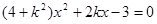 ,根据韦达定理,即可求实数
,根据韦达定理,即可求实数 的值.
的值.
试题解析:(1)设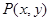 ,由椭圆定义可知,点
,由椭圆定义可知,点 的轨迹
的轨迹 是以
是以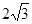 为焦距,长半轴为
为焦距,长半轴为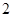 的椭圆.它的短半轴
的椭圆.它的短半轴 ,故曲线C的方程为
,故曲线C的方程为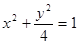 .
.
(2)设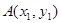 ,
,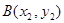 ,其坐标满足
,其坐标满足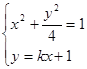 ,
,
消去 并整理得
并整理得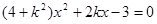 , (*)
, (*)
故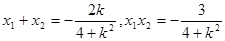 .
.
若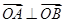 ,即
,即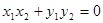 ,即
,即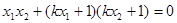 ,化简得
,化简得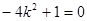 ,所以
,所以 满足(*)中
满足(*)中 ,故
,故 即为所求.
即为所求.
考点:轨迹方程;平面向量数量积的运算.

练习册系列答案
相关题目
 中,如图E、F分别是
中,如图E、F分别是  ,CD的中点,
,CD的中点, ;
; .
. 

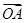 =-2
=-2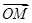 ,求证:
,求证: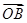 +
+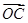 =0;
=0;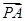 ·(
·(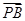 +
+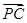 )的最小值.
)的最小值. ·
· =
= ·
· =k(k∈R).
=k(k∈R). 两点分别在射线
两点分别在射线 上移动,
上移动, ,
, 为坐标原点,动点
为坐标原点,动点 满足
满足

 的方程;
的方程;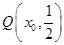 ,过
,过 作(1)中曲线
作(1)中曲线 ,①求证:直线
,①求证:直线 过定点;
过定点; ,求
,求 的值。
的值。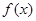 的对称轴方程为:
的对称轴方程为: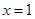 ,设向量
,设向量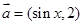 ,
,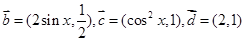 .
.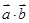 和
和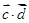 的取值范围;
的取值范围; 时,求不等式
时,求不等式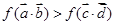 的解集.
的解集.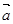 、
、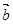 、
、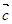 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中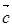 |
|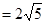 ,且
,且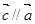 ,求
,求 且
且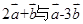 垂直,求
垂直,求 的圆周上.从整点
的圆周上.从整点 到整点
到整点 的向量记作
的向量记作 ,则
,则 = .
= .