题目内容
已知a=(1,2),b=(-2,n) (n>1),a与b的夹角是45°.
(1)求b;
(2)若c与b同向,且a与c-a垂直,求c.
(1) b=(-2,6) (2) (-1,3).
解析试题分析:(1)利用向量夹角公式可得关于n的方程,解出n即得向量b;
(2)由c与b同向,同向,可设c=λb (λ>0),利用向量垂直的充要条件可求得λ,代入即可求得c;
(1)a·b=2n-2,|a|=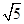 ,|b|=
,|b|=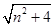 ,
,
∴cos 45°=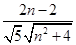 =
=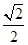 ,∴3n2-16n-12=0,∴n=6或n=-
,∴3n2-16n-12=0,∴n=6或n=-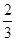 (舍),∴b=(-2,6).
(舍),∴b=(-2,6).
(2)由(1)知,a·b=10,|a|2=5.又c与b同向,故可设c=λb (λ>0),(c-a)·a=0,
∴λb·a-|a|2=0,∴λ= =
=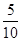 =
=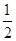 ,∴c=
,∴c=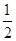 b=(-1,3).
b=(-1,3).
考点:平面向量数量积的运算;利用数量积判断两向量的垂直关系.

练习册系列答案
相关题目
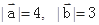 .(1)若
.(1)若 的夹角为60o,求
的夹角为60o,求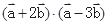 ;
;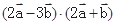 =61,求
=61,求
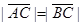 ,求
,求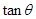 的值;
的值;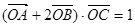 ,其中
,其中 为坐标原点,求
为坐标原点,求 的值.
的值. 中,动点
中,动点 到两点
到两点 、
、 的距离之和等于4.设点
的距离之和等于4.设点 .
.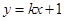 与
与 、
、 两点,若
两点,若 ,求
,求 的值.
的值.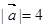 ,
,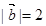 ,且
,且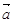 与
与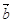 夹角为120°求
夹角为120°求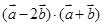 ; (2)
; (2)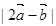 ; (3)
; (3) 的夹角
的夹角 的准线上,且椭圆C过点
的准线上,且椭圆C过点 .
. 作直线
作直线 与椭圆C相交于E,F两点,直线AE,AF与直线
与椭圆C相交于E,F两点,直线AE,AF与直线 分别交于不同的两点M,N,求
分别交于不同的两点M,N,求 的取值范围.
的取值范围.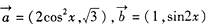 ,函数
,函数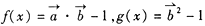
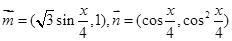 。
。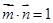 ,求
,求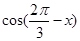 的值;
的值;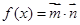 ,在
,在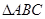 中,角
中,角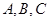 的对边分别是
的对边分别是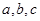 ,且满足
,且满足 ,求函数
,求函数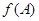 的取值范围。
的取值范围。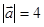 ,
,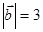 ,
,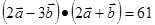 ,则
,则 与
与 的夹角
的夹角 为
为