题目内容
如图: 两点分别在射线
两点分别在射线 上移动,
上移动,
且 ,
, 为坐标原点,动点
为坐标原点,动点 满足
满足

(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)设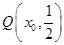 ,过
,过 作(1)中曲线
作(1)中曲线 的两条切线,切点分别
的两条切线,切点分别
为 ,①求证:直线
,①求证:直线 过定点;
过定点;
②若 ,求
,求 的值。
的值。
(1) ;(2)②
;(2)② .
.
解析试题分析:(1) 设动点 的坐标为
的坐标为 ,由
,由

另由

于是由此可消去上参数方程中的参数而得点 的轨迹方程.
的轨迹方程.
(2)①设 ,先用导数求出双曲线在
,先用导数求出双曲线在 处的切线,利用两切线均过点
处的切线,利用两切线均过点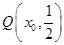 得到直线
得到直线 的方程并进一步证明其过定点.
的方程并进一步证明其过定点.
②由①可知,设直线 的方程为
的方程为 ,易知
,易知 且
且 ,
,
所以可利用方程组 消去
消去 得
得 ,再结合韦达定理解决.
,再结合韦达定理解决.
解:(1)由已知得, ,即
,即
设 坐标为
坐标为 ,由
,由 得:
得:
∴ ,消去
,消去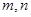 可得,
可得,
∴轨迹 的方程为:
的方程为: 4分
4分
(2)①由(1)知, 即
即
设 ,则
,则 ,
,
∴ ,即
,即 ,
,
∵ 在直线
在直线 上,∴
上,∴ ⑴同理可得,
⑴同理可得, ⑵
⑵
由⑴⑵可知, ∴直线
∴直线 过定点
过定点 9分
9分
②由①可知,设直线 的方程为
的方程为 ,易知
,易知 且
且 ,将直线
,将直线 的方程代入曲线C的方程得:
的方程代入曲线C的方程得:
∴
又
 即
即 ∴
∴ 13分
13分
考点:1、动点轨迹方程的求法;2、平面向量的数量积;3、直线与圆锥曲线的综合问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.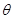 为向量
为向量 与向量
与向量 的夹角,求
的夹角,求 垂直,求
垂直,求 的值.
的值. 中,动点
中,动点 到两点
到两点 、
、 的距离之和等于4.设点
的距离之和等于4.设点 .
.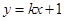 与
与 、
、 两点,若
两点,若 ,求
,求 的值.
的值.
 ,求x的范围;
,求x的范围; 的最大值以及此时x的值.
的最大值以及此时x的值. 的准线上,且椭圆C过点
的准线上,且椭圆C过点 .
. 作直线
作直线 与椭圆C相交于E,F两点,直线AE,AF与直线
与椭圆C相交于E,F两点,直线AE,AF与直线 分别交于不同的两点M,N,求
分别交于不同的两点M,N,求 的取值范围.
的取值范围.
 ,
,
 ,
,  的值。
的值。 为何值时,
为何值时,
 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向? ,
, .
. ,
, ,且
,且 ,求
,求 ;
; ,求
,求 的取值范围.
的取值范围.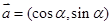 ,
, .
. ,求
,求 的值;
的值; ,
, 求
求 的值.
的值.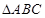 中,
中,
 ,则
,则 __________;
__________;