题目内容
在正方体 中,如图E、F分别是
中,如图E、F分别是  ,CD的中点,
,CD的中点,
(1)求证: ;
;
(2)求 .
. 
(1)证明见解析;(2)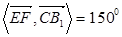 .
.
解析试题分析:(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明证线线垂直,只需要证明直线的方向向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:解:建立如图所示的直角坐标系,(1)不妨设正方体的棱长为1,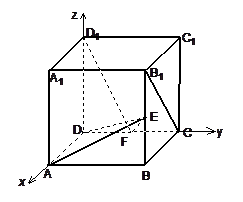
则D(0,0,0),A(1,0,0),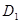 (0,0,1),
(0,0,1),
E(1,1, ),F(0,
),F(0, ,0),
,0),
则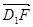 =(0,
=(0, ,-1),
,-1),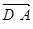 =(1,0,0),
=(1,0,0), 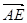 =(0,1,
=(0,1, ),
), 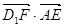 =0,
=0,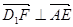 .
.
(2)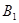 (1,1,1),C(0,1,0),故
(1,1,1),C(0,1,0),故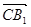 =(1,0,1),
=(1,0,1),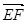 =(-1,-
=(-1,- ,-
,- ),
),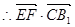 =-1+0-
=-1+0- =-
=- ,
, 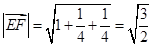 ,
,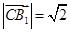 ,
,
则cos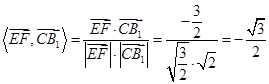 .
.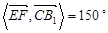 .
.
考点:利用空间向量证明线线垂直和求夹角.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 内接于以
内接于以 为圆心,半径为1的圆,且
为圆心,半径为1的圆,且
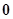 ,则
,则 的面积为 .
的面积为 . ,
, 表示
表示 ,
, ;
;
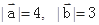 .(1)若
.(1)若 的夹角为60o,求
的夹角为60o,求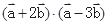 ;
;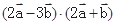 =61,求
=61,求 .
.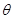 为向量
为向量 与向量
与向量 的夹角,求
的夹角,求 垂直,求
垂直,求 的值.
的值. 中,动点
中,动点 到两点
到两点 、
、 的距离之和等于4.设点
的距离之和等于4.设点 .
.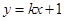 与
与 、
、 两点,若
两点,若 ,求
,求 的值.
的值. ,
, .
. ,
, ,且
,且 ,求
,求 ;
; ,求
,求 的取值范围.
的取值范围.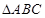 中,
中,
 ,则
,则 __________;
__________; 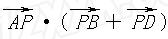 的取值范围是________.
的取值范围是________.