题目内容
【题目】双曲线C： 
﹣ 
=1（a＞0，b＞0）两条渐近线l1 ， l2与抛物线y2=﹣4x的准线1围成区域Ω，对于区域Ω（包含边界），对于区域Ω内任意一点（x，y），若 
的最大值小于0，则双曲线C的离心率e的取值范围为 ．
【答案】（1， 
）
【解析】解：双曲线C： 
﹣ 
=1的渐近线方程为y=± 
x，
抛物线y2=﹣4x的准线1：x=1，
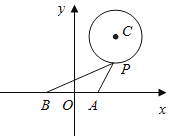
渐近线l1 ， l2与抛物线y2=﹣4x的准线1围成区域Ω，如图，
= 
﹣1的几何意义是点（x，y）
与点P（﹣3，﹣1）的斜率与1的差，
求得A（1， ），B（1，﹣ ），
连接PA，可得斜率最大为 
，
由题意可得 ﹣1＜0，
可得 ＜3，即3a＞b，9a2＞b2=c2﹣a2 ，
即c2＜10a2 ， 即有c＜ a．
可得1＜e＜ ．
所以答案是：（1， ）．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某高级中学在今年“五一”期间给校内所有教室安装了同一型号的空调，关于这批空调的使用年限
单位：年
和所支出的维护费用
单位：千元厂家提供的统计资料如表：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
若x与y之间是线性相关关系，请求出维护费用y关于x的线性回归直线方程
；
若规定当维护费用y超过
千元时，该批空调必须报度，试根据的结论求该批空调使用年限的最大值
结果取整数参考公式：
，
．
