题目内容
【题目】在直三棱柱ABC-A1B1C1中,AC=BC=AB=2,AA1=3，D点是AB的中点
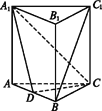
（1）求证:BC1∥平面CA1D．
（2）求三棱锥B-A1DC的体积．
【答案】（1）见证明；（2）
【解析】
(1) 连接AC1交A1C于点E，连接DE，由直三棱柱的几何特征及三角形中位线定理，可得DE∥BC1，进而由线面平行的判定定理得到结论；
(2) 三棱锥B1﹣A1DC的体积
=
，求出棱锥的底面面积和高，代入棱锥体积公式，可得答案．
（1）证明：连接AC1 交AC于E点，连接DE
∵ABC-A1B1C1为直三棱柱，故AA1C1C为矩形
∴E是AB的中点
又∵D点是AB的中点
∴DE∥BC1
又DE在平面CA1D内
∴BC1∥平面CA1D.
（2）三棱锥B-A1DC的体积即为三棱锥A1-BDC的体积.
由题易得三棱锥A1-BDC的高h=A A1=3
又∵AB=BC=AC=2，D为AB的中点
∴三角形ABC的面积S=
AB
CD
=
∴三棱锥A1-BDC的体积
V=
Sh=
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某企业常年生产一种出口产品，根据预测可知，进入21世纪以来，该产品的产量平稳增长．记2009年为第1年，且前4年中，第x年与年产量f(x) 万件之间的关系如下表所示：
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一：f(x)＝ax＋b，f(x)＝2x＋a，f(x)＝log
x＋a.
(1)找出你认为最适合的函数模型，并说明理由，然后选取其中你认为最适合的数据求出相应的解析式；
(2)因遭受某国对该产品进行反倾销的影响，2015年的年产量比预计减少30%，试根据所建立的函数模型，确定2015年的年产量．