题目内容
【题目】曲线![]() 与两坐标轴的交点都在圆
与两坐标轴的交点都在圆![]() 上,圆
上,圆![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴分别交于
轴正半轴分别交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,是否存在
两点,是否存在![]() 使得
使得![]() 与
与![]() 共线,如果存在求直线
共线,如果存在求直线![]() 的方程,若不存在请说明理由.
的方程,若不存在请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)存在,方程为
;(Ⅱ)存在,方程为![]() .
.
【解析】
(Ⅰ)令![]() ,则
,则![]() 或
或![]() ,令
,令![]() ,则
,则![]() ,得到曲线与坐标轴交点为
,得到曲线与坐标轴交点为![]() ,
,![]() ,
,![]() ,再求圆的方程.
,再求圆的方程.
(Ⅱ)假设存在![]() 满足条件,当
满足条件,当![]() 的斜率不存在时,不满足条件,当斜率存在时,设
的斜率不存在时,不满足条件,当斜率存在时,设![]() 的方程为
的方程为![]() ,联立
,联立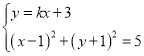 得
得![]() ,设
,设![]() ,
,![]() ,利用韦达定理求得
,利用韦达定理求得 ![]() 的坐标,再根据共线向量定理求解.
的坐标,再根据共线向量定理求解.
(Ⅰ)令![]() ,则
,则![]() 或
或![]() ,
,
令![]() ,则
,则![]() ,
,
曲线与坐标轴交点为![]() ,
,![]() ,
,![]() ,
,
设圆心为![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
∴圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)假设存在![]() 满足条件,
满足条件,
当![]() 的斜率不存在时,不满足条件,
的斜率不存在时,不满足条件,
当![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,
,
由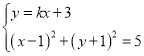 得
得![]() ,
,
![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]()
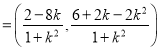 ,
,
由(1)知![]() ,
,![]() ,
,
∴![]() ,
,
若![]() 与
与![]() 共线,则
共线,则![]() ,
,
整理得![]() ,
,
∴![]() 或
或![]() ,
,
经检验![]() ,符合
,符合![]() ,
,
∴存在![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目
【题目】交通部门调查在高速公路上的平均车速情况,随机抽查了60名家庭轿车驾驶员,统计其中有40名男性驾驶员,其中平均车速超过![]() 的有30人,不超过
的有30人,不超过![]() 的有10人;在其余20名女性驾驶员中,平均车速超过
的有10人;在其余20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(1)完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为,家庭轿车平均车速超过
的把握认为,家庭轿车平均车速超过![]() 与驾驶员的性别有关;
与驾驶员的性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员 | |||
女性驾驶员 | |||
合计 |
(2)根据这些样本数据来估计总体,随机调查3辆家庭轿车,记这3辆车中,驾驶员为女性且平均车速不超过![]() 的人数为
的人数为![]() ,假定抽取的结果相互独立,求
,假定抽取的结果相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: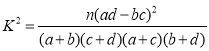
![]()
临界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |